GeoGebra online, cách sử dụng GeoGebra cơ bản để vẽ hình, vẽ đồ thị trực quan

GeoGebra là gì?

• Phần mềm toán học năng động sử dụng dễ dàng.
• Cho học và giảng dạy ở nhiều cấp học.
• Kết hợp hình học, đại số, bảng biểu, tính toán, đồ họa và thống kê trong môi trường 2D và 3D.
• Có sẵn phần mềm miễn phí trên geogebra.org.

Cụ thể hơn, GeoGebra tạo điều kiện cho sáng tạo ra các mô hình, hình học toán học cho học sinh. Nó cho phép trải nghiệm khám phá qua các tương tác như di chuyển đối tượng và thay đổi các thông số.

GeoGebra cũng là một công cụ soạn bài cho giáo viên để tạo những bài tập, câu hỏi tương tác cho học sinh. Bạn có thể tìm những tài liệu học miễn phí và chia sẻ bài giảng của mình trên geogbratube.org. GeoGebra có sẵn bản cài trên máy tính: tải GeoGebra về máy tính hoặc sử dụng GeoGebra trực tuyến.

Bắt đầu nhanh với GeoGebra, GeoGebra Online

Nếu không cài GeoGebra bạn có thể truy cập GeoGebra Online. Trong bài viết này Quantrimang.com sẽ hướng dẫn bạn sử dụng GeoGebra bản cài trên máy tính để vẽ hình.

Bức ảnh ở trên là màn hình chính của GeoGebra. Dựa vào mục đích sử dụng GeoGebra, bạn có thể lựa chọn bố cục tương đương từ menu Perspectives. Theo mặc định, phần Algebra View (Đại số) và phần Graphics View (Hình học) được hiển thị trong cửa sổ GeoGebra.

Thanh Toolbar là tập hợp những hộp công cụ, mỗi hộp chứa những công cụ có liên quan đến nhau. Nhờ những công cụ này, bạn có thể tạo ra rất nhiều dạng hình học khác nhau trong phần Graphics View chỉ với những cú nhấp chuột. Đồng thời, các tọa độ và phương trình tương ứng sẽ hiển thị ở phần Algebra View. Chú ý, mỗi phần có thanh công cụ điều chỉnh riêng.

Thanh Input Bar ở cuối cửa sổ GeoGebra sử dụng để nhập trực tiếp các tọa độ, phương trình, dấu, hoặc hàm. Sau khi ấn Enter, biểu thị đại số sẽ hiển thị trong phần Algebra View, và biểu thị đồ thị hiển thị trong phần Graphics View.

Hơn nữa, GeoGebra cung cấp hình ảnh đồ họa 3D và CAS để sử dụng hệ thống đại số trên máy tính của GeoGebra, và Spreadsheet View sẽ làm việc với dữ liệu và các khái niệm thống kê, giống như chiếc máy tính xác suất để tính toán và phân phối đồ thị xác suất.

Tất cả các phần của GeoGebra được liên kết mật thiết, nghĩa là nếu bạn thay đổi đối tượng nào đó thì những biểu thị trong những phần còn lại tự động thay đổi.

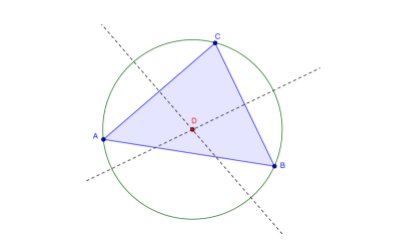
Ví dụ 1: Hình tròn ngoại tiếp tam giác.

Bài tập: Dựng hình tam giác ABC và đường tròn ngoại tiếp sử dụng GeoGebra.

Chuẩn bị:

• Khởi động cửa sổ mới GeoGebra.
• Click vào mũi tên ở phía bên phải của Graphics View để mở thanh Perspectives và chọn Geometry Perspective.
• Làm quen với các công cụ được cung cấp trong Graphics View Toolbar. Gợi ý: bạn có thể mở hộp công cụ bằng cách click vào mũi tên nhỏ ở phía dưới góc bên phải của thanh công cụ chính.

Các bước lập:

1. Chọn Polygon từ thanh Toolbar. Bây giờ, click ba lần vào Graphics View theo chiều kim đồng hồ để tạo 3 điểm A, B, C. Khóa hình tam giác đã tạo bằng cách ấn lại vào điểm A một lần nữa.
2. Chọn Perpendicular Bisector và tạo hai đường phân giác bằng cách click vào 2 cạnh của tam giác. Lưu ý: có thể tìm thấy công cụ ở hộp công cụ.
3. Sử dụng Intersect bạn có thể nhấp chuột vào đường phân giác để tạo tâm đường tròn.
4. Lựa chọn Circle with Center through Point. Đầu tiên click lần lượt vào tâm điểm và các đỉnh của tam giác để tạo đường tròn ngoại tiếp tam giác.
5. Công cụ di chuyển Move sử dụng chuột để kéo các đỉnh của tam giác. Cấu trúc của hình sẽ thay đổi trong khi bạn di chuyển. Chú ý: để chuyển toàn bộ hình trong Graphics View, chọn công cụ Move Graphics View rồi kéo hình.

Chú ý:

• Có các nút Undo/Redo ở bên phải của thanh công cụ.
• Sử dụng các nút Show / Hide Object từ Graphics View Toolbar để ẩn và hiện một vật. Chọn tất cả các hình bạn muốn ẩn, sau đó, chuyển tới công cụ khác để áp dụng sự thay đổi của bạn.
• Bạn có thể thay đổi hình dạng của hình. (Ví dụ: thay đổi màu sắc hoặc đường viền, ẩn/ hiện nhãn) dễ dàng sử dụng bằng Style Bar. Chọn vật bạn muốn chỉnh sửa và click mũi tên nhỏ ở góc trên bên phải của phần hình học để mở Style Bar.

• Bạn có thể ấn/hiện axes (hệ trục) và grid (đường kẻ ô) của Style Bar với cách tương tự ở trên.
• Construction Protocol trên thanh menu cung cấp bảng danh sách tất cả các bước lập. Hơn nữa, bạn có thể thay đổi thứ tự các bước thiết lập bằng cách kéo các dòng lên hoặc xuống.

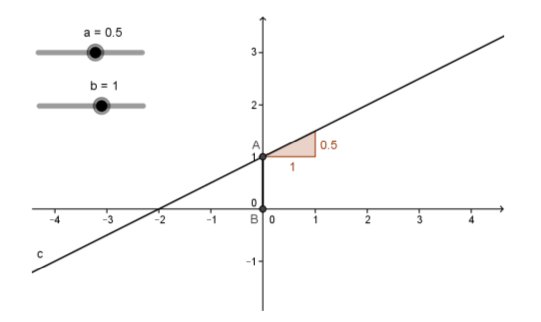
Ví dụ 2: Phương trình tuyến tính

Bài tập: Sử dụng thanh trượt để thay đổi thông số của phương trình tuyến tính.

Chuẩn bị:

• Mở cửa sổ mới của GeoGebra sử dụng menu File.
• Click vào mũi tên phía bên phải của Graphics View để có Perspectives sidebar và chọn Algebra Perspective.

Các bước lập:

1. Nhập y = 0.8 * x + 3.2 vào Input Bar và ấn Enter.
2. Mở rộng: Thông số nào có thể được thay đổi khi bạn sửa đổi phương trình đường thẳng trong Algebra View (sử dụng nút mũi tên) hoặc đường kẻ ở Graphics View (sử dụng chuột). Lưu ý: Chắc chắn đã lựa chọn phương trình hoặc đường thằng trước khi thiết lập.
3. Trong Graphics View, sử dụng công cụ Delete trong hộp công cụ để xóa đường thẳng.
4. Sử dụng Slider tool để tạo thanh trượt a và b.
5. Nhập y = a*x + b vào Input Bar và ấn Enter.
6. Chọn Intersect từ Graphics View tạo điểm giao nhau A giữa các đường thẳng và trục hoành.
7. Sử dụng Point on Object tạo điểm B ở gốc tọa độ.
8. Sử dụng Segment vẽ đoạn thẳng giữa 2 điểm A và B.
9. Sử dụng công cụ Slope để tạo đường chéo.

Chú ý:

Bạn muốn sửa đổi hình dạng của hình sử dụng Input Bar. Lựa chọn vật bạn muốn sửa và sau đó click mũi tên nhỏ ở góc trên bên phải của Graphics View để mở thanh tạo kiểu.

Ví dụ 3: Giao điểm của những hàm đa thức

Bài tập: Một Parabal có thể giao nhau với phương trình đường thẳng bằng cách xác định nghiệm phân biệt.

Chuẩn bị:

• Khởi động cửa sổ GeoGebra sử dụng menu File.
• Lựa chọn mũi tên bên phải của phần hình học để mở thanh Perspectives sidebar và chọn bố cục CAS.

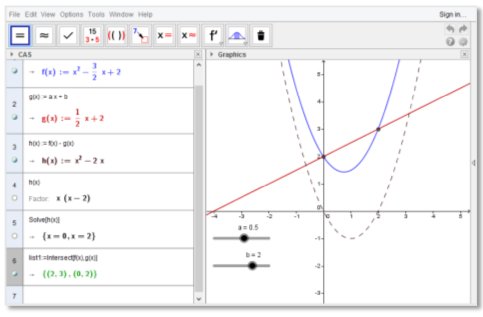
Các bước thiết lập

1. Phần CAS, tạo một đa thức bậc hai bằng cách nhập f(x):=x^2 – 3/2 * x + 2 vào dòng đầu tiên và ấn enter.
2. Chọn công cụ trượt tử thanh công cụ phần hình học và tạo hai thanh trượt a và b. Chú ý: Sau khi chọn phần hình học, một cửa sổ mới xuất hiện cho phép bạn chỉ định các thông số thanh trượt. Click áp dụng để đóng cửa sổ và một thanh trượt.
3. Phần CAS, tạo phương trình đường thẳng bằng cách nhập g(x):= a*x + b ở dòng tiếp theo và ấn enter.
4. Trong phần hình học, sử dụng công cụ di chuyển để thay đổi giá trí của thanh trượt a lên 0,5 và giá trị thanh trượt của b là 2.
5. Phần CAS nhập h(x) := f(x) – g(x) để xác định khác biệt giữa hai phương trình.
6. Nhập h(x), sau đó lựa chọn công cụ hệ số từ thanh công cụ của phần CAS để tìm thừa số của đa thức. Bạn có thể sử dụng những hệ số khác để xác định gốc của h(x).
7. Nhập solve [h(x)], sau đó xác nhận các gốc. Chú ý: GeoGebra tạo danh sách các điểm có thể hiện thị trong phần hình học bằng cách click biểu tượng hiện đối tượng phía dưới số dòng tượng tự của phần CAS.
8. Nhập Intersect [f(x),g(x)] để tạo giao điểm của các phương trình. Bạn có thể hiển thị điểm giao nhau trong phần hình học bằng cash lựa chọn biểu tượng ấn/hiện ở số dòng tương tự trong phần CAS.
9. Hãy cố gắng tìm ra những giao điểm của f(x) và g(x) có điểm chung với những gốc của hàm h(x) khác. Thay đổi thông số của phương trình đường thẳng để tìm giá trị của a và b và chúng sẽ có hai, một hoặc không có giao điểm. Chú ý: sử dụng công cụ di chuyển để thay đổi giá trị của thanh trượt và tạo một phương trình mới.

Lưu ý:

Phần CAS cho phép bạn làm việc với phân số, phương trình hoặc phép tính....

Đầu vào và tự động hoàn thành.

• Nhập y = 2x + 1 để xác định phương trình.
• Nhập f(x) := 2x + 1 để quy ước tên của phương trình.
• Nếu bạn nhập dấu ngoặc đơn hoặc ngoặc kép, GeoGebra sẽ tự động chèn bản sao kín tương ứng.
• Trong khi nhập một lệnh vào phần CAS, GeoGebra sẽ cố gắng hoàn thành lệnh tự dộng để hỗ trợ các cú pháp. Chú ý: chọn lệnh bạn muốn từ danh sách hiện ra và ấn enter để chấp nhận gợi ý.
• Thanh công cụ yêu cầu ba công cụ khác nhau để đánh giá đầu vào của bạn. "Đánh giá" tính và đơn giản hóa đầu vào bằng các biểu tượng. "Con số" tính đầu vào số và cho ra kết quả trong ký hiệu thập phân. "Giữ đầu vào" giữ và kiểm tra đầu vào. Công cụ này rất hữu ích nếu bạn muốn đầu vào của bạn được đơn giản hóa một cách tự động. Ví dụ, khi giới thiệu các thao tác của biểu thức.
• Bạn chỉ có thể thao tác một phần của biểu thức bằng cách lựa chọn nó và chọn công cụ yếu tố.