Công thức tính thể tích khối trụ và ví dụ minh họa

PP

Hình trụ tròn là hình có hai mặt đáy là hai hình tròn song song với nhau và bằng nhau. Trong cuộc sống, các đồ vật hình trụ tròn gồm có lon sữa bò, cái cốc, lọ hoa, cái thùng, cái xô...

Thể tích hình trụ

Công thức tính thể tích hình trụ
Các khái niệm về hình trụ, mặt trụ, khối trụ
Tính thể tích hình trụ

Công thức tính thể tích hình trụ

Muốn tính thể tích của hình trụ, ta lấy chiều cao nhân với bình phương độ dài bán kính hình tròn mặt đáy hình trụ và số pi.

$V=\pi .r^{2} .h$

Trong đó:

V là thể tích hình trụ.
r là bán kính hình trụ.
h là chiều cao, khoảng cách giữa 2 đáy của hình trụ.
Đơn vị thể tích: mét khối (m³)

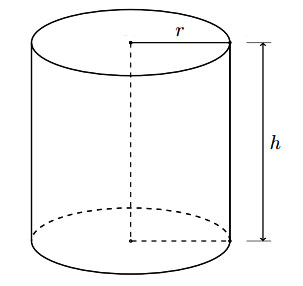Các bạn có thể xem lại công thức tính diện tích xung quanh hình trụ và diện tích toàn phần hình trụ.

Các khái niệm về hình trụ, mặt trụ, khối trụ

1. Mặt trụ

Trong mặt phẳng $(P)$ cho hai đường thẳng $∆$ và $l$ song song nhau, cách nhau một khoảng $r$ . Khi quay $(P)$ quanh trục cố định $∆$ thì đường thẳng $l$ sinh ra một mặt nón tròn xoay được gọi là mặt trụ tròn xoay hay gọi tắt là mặt trụ.
Đường thẳng $∆$ gọi là trục, đường thẳng $l$ gọi là đường sinh và khoảng cách $r$ gọi là bán kính của mặt trụ.

2. Hình trụ

Khi quay hình chữ nhật $ABCD$ quanh cạnh $AB$ thì đường gấp khúc $ABCD$ tạo thành một hình được gọi là hình trụ tròn xoay hay gọi tắt là hình trụ.
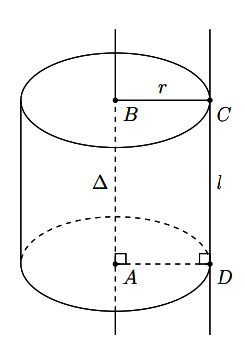Đường thẳng $AB$ gọi là trục, đoạn thẳng $CD$ gọi là đường sinh, độ dài $AB = CD$ gọi là chiều cao, hai hình tròn $(A; AD)$ và $(B; BC)$ gọi là hai đáy của hình trụ.

3. Khối trụ

Khối trụ tròn xoay, gọi tắt là khối trụ là phần không gian giới hạn bởi hình trụ tròn xoay, kể cả hình trụ.
Thể tích khối trụ là lượng không gian mà hình trụ chiếm.

4. Diện tích xung quanh hình trụ

- Diện tích xung quanh hình trụ bằng chu vi đáy nhân với đường cao.

${S_{xq}} = 2\pi rh$

5. Diện tích toàn phần hình trụ

Diện tích toàn phần bằng diện tích xung quanh cộng với diện tích của hai đáy.

${S_{tp}} = {S_{xq}} + 2.{S_d} = 2\pi rh + 2.\pi {r^2}$

Tính thể tích hình trụ

Bài 1: Tính thể tích của hình trụ biết bán kính hai mặt đáy bằng $7,1 cm$ ; chiều cao bằng $5 cm$ .

Giải:

Ta có $V=πr^²h$

Thể tích của hình trụ là: $3,14 . (7,1)^² . 5 = 791,437 (cm^³)$

Bài 2: Một hình trụ có diện tích xung quanh là $20π cm^²$ và diện tích toàn phần là $28π cm^²$ . Tính thể tích của hình trụ đó.

Giải:

Diện tích toàn phần hình trụ là $S_{tp} = S_{xq} + S_đ = 2πrh + 2πr^²$

Suy ra $2πr^² = 28π - 20π = 8π$

Do đó $r = 2cm$

Diện tích xung quanh hình trụ là $S_{xq} = 2πrh$

$<=> 20π = 2π.2.h$
$<=> h = 5cm$

Thể tích hình trụ là $V = πr^²h = π.22.5 = 20π (cm^³)$

Bài 3: Một hình trụ có chu vi đáy bằng $20 cm$ , diện tích xung quanh bằng $14 cm^²$ . Tính chiều cao của hình trụ và thể tích của hình trụ.

Giải:

Chu vi đáy của hình trụ là chu vi của hình tròn

$C= 2rπ = 20 cm$

$=>2rπ = 20 => r \approx 3,18 cm$

Diện tích xung quanh của hình trụ:

$S_{xq} = 2πrh= 20 . h = 14$
$\Rightarrow h = \frac{{14}}{{20}} = 0,7\left( {cm} \right)$

Thể tích của hình trụ: $V = π r^² . h \approx 219,91 cm^³$

Thứ Bảy, 16/08/2025 06:03

3,5 ★ 24 👨 512.181

Bạn nên đọc

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!