Giải thuật tìm kiếm theo chiều sâu

Giải thuật tìm kiếm theo chiều sâu là gì?

Giải thuật tìm kiếm theo chiều sâu (Depth First Search – viết tắt là DFS), còn được gọi là giải thuật tìm kiếm ưu tiên chiều sâu, là giải thuật duyệt hoặc tìm kiếm trên một cây hoặc một đồ thị và sử dụng stack (ngăn xếp) để ghi nhớ đỉnh liền kề để bắt đầu việc tìm kiếm khi không gặp được đỉnh liền kề trong bất kỳ vòng lặp nào. Giải thuật tiếp tục cho tới khi gặp được đỉnh cần tìm hoặc tới một nút không có con. Khi đó giải thuật quay lui về đỉnh vừa mới tìm kiếm ở bước trước.

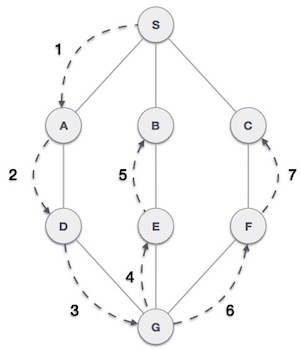
Trong hình minh họa trên, giải thuật tìm kiếm theo chiều sâu đầu tiên duyệt từ các đỉnh A tới B tới C tới D sau đó tới E, sau đó tới F và cuối cùng tới G. Giải thuật này tuân theo qui tắc sau:

Qui tắc 1: Duyệt tiếp tới đỉnh liền kề mà chưa được duyệt. Đánh dấu đỉnh mà đã được duyệt. Hiển thị đỉnh đó và đẩy vào trong một ngăn xếp (stack).

Qui tắc 2: Nếu không tìm thấy đỉnh liền kề, thì lấy một đỉnh từ trong ngăn xếp (thao tác pop up). (Giải thuật sẽ lấy tất cả các đỉnh từ trong ngăn xếp mà không có các đỉnh liền kề nào)

Qui tắc 3: Lặp lại các qui tắc 1 và qui tắc 2 cho tới khi ngăn xếp là trống.

Bảng dưới đây minh họa các qui tắc với hình ví dụ trên:

Khởi tạo ngăn xếp (stack)

Đánh dấu đỉnh S là đã duyệt và đặt đỉnh này vào trong ngăn xếp. Tìm kiếm bất kỳ đỉnh liền kề nào mà chưa được duyệt từ đỉnh S. Chúng ta có 3 đỉnh và chúng ta có thể lấy bất kỳ đỉnh nào trong số chúng. Ví dụ, chúng ta lấy đỉnh A theo thứ tự chữ cái.

Đánh dấu đỉnh A là đã duyệt và đặt vào trong ngăn xếp. Tìm kiếm bất kỳ đỉnh liền kề nào với đỉnh A. Cả S và D đều là hai đỉnh liền kề A nhưng chúng ta chỉ quan tâm về đỉnh chưa được duyệt.

Duyệt đỉnh D, đánh dấu đỉnh này là đã duyệt và đặt vào trong ngăn xếp. Ở đây, chúng ta có B và C là hai đỉnh kề với D và cả hai đều là chưa được duyệt. Chúng ta sẽ chọn theo thứ tự chữ cái một lần nữa.

Chọn B, đánh dấu là đã duyệt và đặt vào trong ngăn xếp. Ở đây B không có bất kỳ đỉnh liền kề nào mà chưa được duyệt. Vì thế chúng ta lấy B ra khỏi ngăn xếp.

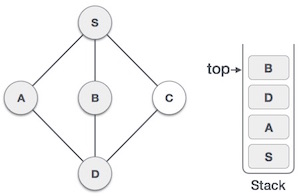
Kiểm tra phần tử trên cùng của ngăn xếp để trở về nút đã duyệt trước đó và kiểm tra xem đỉnh này có đỉnh nào liền kề mà chưa được duyệt hay không. Ở đây, chúng ta tìm thấy đỉnh D nằm ở trên cùng của ngăn xếp.

Chỉ có một đỉnh liền kề với D mà chưa được duyệt, đó là đỉnh C. Chúng ta duyệt C, đánh dấu là đã duyệt và đặt vào trong ngăn xếp.

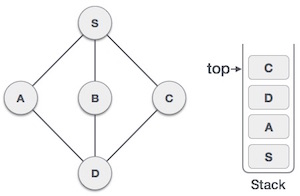
Vì C không có bất kỳ đỉnh nào liền kề mà chưa được duyệt, chúng ta tiếp tục lấy các đỉnh từ trong ngăn xếp để tìm xem có còn bất kỳ đỉnh nào liền kề mà chưa được duyệt hay không. Trong ví dụ này là không có, và chúng ta vẫn tiếp tục cho tới khi ngăn xếp là trống.

Theo Tutorialspoint

Bài trước: Cấu trúc dữ liệu đồ thị (Graph)

Bài tiếp: Giải thuật tìm kiếm theo chiều rộng