Cấu trúc dữ liệu Heap
Cấu trúc dữ liệu Heap là gì?
Cấu trúc dữ liệu Heap là một trường hợp đặc biệt của cấu trúc dữ liệu cây nhị phân cân bằng, trong đó khóa của nút gốc được so sánh với các con của nó và được sắp xếp một cách phù hợp. Nếu α có nút con β thì:
key(α) ≥ key(β)
Khi giá trị của nút cha lớn hơn giá trị của nút con, thì thuộc tính này tạo ra một Max Heap. Dựa trên tiêu chí này, một Heap có thể là một trong hai kiểu sau:
Với dữ liệu đầy vào → 35 33 42 10 14 19 27 44 26 31
Min-Heap: ở đây giá trị của nút gốc là nhỏ hơn hoặc bằng các giá trị của các nút con.
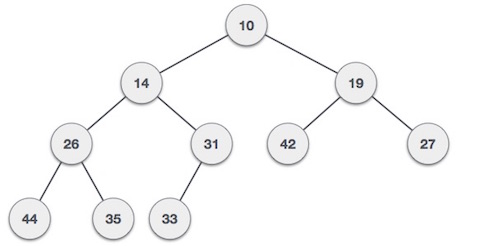
Max-Heap: ở đây giá trị của nút gốc là lớn hơn hoặc bằng giá trị của các nút con.

Hai cây ví dụ trên đều được xây dựng dựa trên cùng một dữ liệu đầu vào và cùng thứ tự.
Giải thuật xây dựng Max Heap
Chúng ta sẽ sử dụng cùng ví dụ trên để minh họa cách tạo một Max Heap. Phương thức để xây dựng Min Heap là tương tự.
Chúng ta sẽ suy ra một giải thuật cho Max Heap bằng việc chèn một phần tử tại một thời điểm. Tại bất cứ thời điểm nào, Heap đều phải duy trì (tuân theo) thuộc tính của nó. Trong quá trình chèn, chúng ta cũng giả sử rằng chúng ta đang chèn một nút vào trong HEAPIFIED Tree.
Bước 1: Tạo một nút mới tại vị trí cuối cùng của Heap. Bước 2: Gán giá trị mới cho nút này. Bước 3: So sánh giá trị của nút con với giá trị cha. Bước 4: Nếu giá trị của cha là nhỏ hơn con thì tráo đổi chúng. Bước 5: Lặp lại bước 3 và 4 cho tới khi vẫn duy trì thuộc tính của Heap.
Ghi chú: Trong giải thuật xây dựng Min Heap, giá trị của nút cha sẽ là nhỏ hơn giá trị của các nút con.
Để rõ hơn về giải thuật xây dựng Max Heap, chúng ta hãy nhìn vào hình minh họa động dưới đây.

Giải thuật xóa trong Max Heap
Hoạt động xóa trong Max (hoặc Min) Heap luôn luôn diễn ra tại nút gốc và để xóa giá trị Lớn nhất (hoặc Nhỏ nhất). Bạn theo dõi giải thuật và hình minh họa động dưới đây để hiểu thêm về giải thuật này.
Bước 1: Xóa nút gốc. Bước 2: Di chuyển phần tử cuối cùng có bậc thấp nhất lên nút gốc. Bước 3: So sánh giá trị của nút con này với giá trị của cha. Bước 4: Nếu giá trị của cha là nhỏ hơn của con thì tráo đổi chúng. Bước 5: Lặp lại bước 3 và 4 cho tới khi vẫn duy trì thuộc tính của Heap.
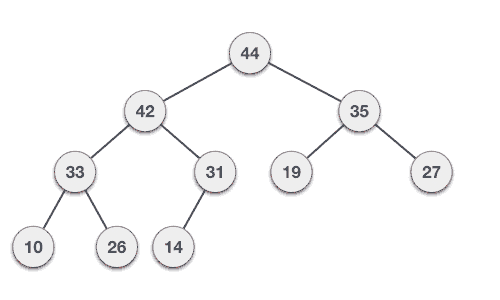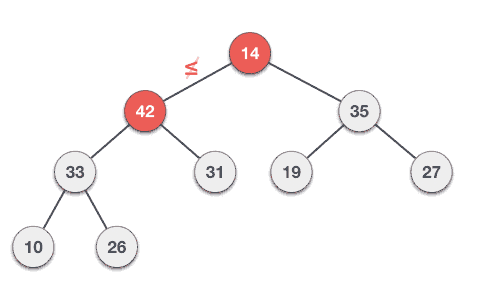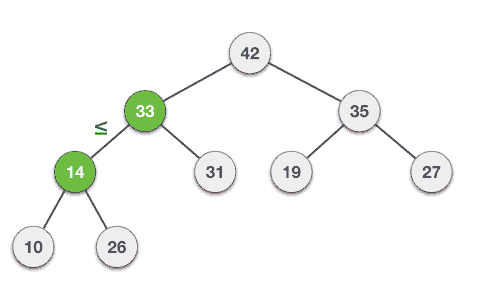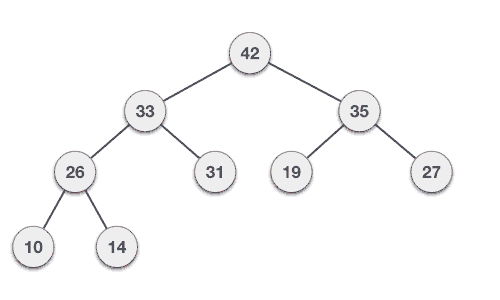
Theo Tutorialspoint
Bài trước: Cây khung (Spanning Tree) trong cấu trúc dữ liệu và giải thuật
Bài tiếp: Khái niệm cơ bản về đệ qui (Recursion)
Bạn nên đọc
-

Cách tính chu vi hình thang: thường, vuông, cân
-

Công thức tính thể tích khối lăng trụ đứng, hình lăng trụ
-

Công thức tính đường cao trong tam giác thường, cân, đều, vuông
-

Công thức tính chu vi hình tam giác
-

Công thức tính diện tích hình Elip
-

Công thức tính đường chéo hình vuông, đường chéo hình chữ nhật
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Cũ vẫn chất
-

Huyền Thoại Hải Tặc - Hải Tặc Đại Chiến
-
Chuyển từ cơ số 2 sang cơ số 16
2 ngày -

Code Skibidi Tower Defense mới nhất và cách đổi code lấy thưởng
2 ngày -

Cách quay video màn hình trên máy Mac
2 ngày -

Cách khôi phục bài viết đã ẩn trên Facebook bằng điện thoại, máy tính
2 ngày 1 -

Top 10+ trang web tốt nhất để tải phụ đề cho phim
3 ngày -

Giải mã bí ẩn đằng sau thủ thuật "lộn chai nước" đang gây "bão" trên thế giới
2 ngày -

Top 5 VPN miễn phí tốt nhất dành cho Windows
2 ngày -

Chào tháng 6: Câu nói hay nhất về tháng 6, stt tháng 6 tràn ngập yêu thương
2 ngày 2 -

Top 9 phần mềm giả lập PC trên Android
2 ngày
 Công nghệ
Công nghệ  AI
AI  Windows
Windows  iPhone
iPhone  Android
Android  Học IT
Học IT  Download
Download  Tiện ích
Tiện ích  Khoa học
Khoa học  Game
Game  Làng CN
Làng CN  Ứng dụng
Ứng dụng 

 Lập trình
Lập trình  Linux
Linux  Đồng hồ thông minh
Đồng hồ thông minh  macOS
macOS  Chụp ảnh - Quay phim
Chụp ảnh - Quay phim  Thủ thuật SEO
Thủ thuật SEO  Phần cứng
Phần cứng  Kiến thức cơ bản
Kiến thức cơ bản  Dịch vụ công trực tuyến
Dịch vụ công trực tuyến  Dịch vụ nhà mạng
Dịch vụ nhà mạng  Quiz công nghệ
Quiz công nghệ  Microsoft Word 2016
Microsoft Word 2016  Microsoft Word 2013
Microsoft Word 2013  Microsoft Word 2007
Microsoft Word 2007  Microsoft Excel 2019
Microsoft Excel 2019  Microsoft Excel 2016
Microsoft Excel 2016  Microsoft PowerPoint 2019
Microsoft PowerPoint 2019  Google Sheets
Google Sheets  Học Photoshop
Học Photoshop  Lập trình Scratch
Lập trình Scratch  Bootstrap
Bootstrap  Năng suất
Năng suất  Game - Trò chơi
Game - Trò chơi  Hệ thống
Hệ thống  Thiết kế & Đồ họa
Thiết kế & Đồ họa  Internet
Internet  Bảo mật, Antivirus
Bảo mật, Antivirus  Doanh nghiệp
Doanh nghiệp  Ảnh & Video
Ảnh & Video  Giải trí & Âm nhạc
Giải trí & Âm nhạc  Mạng xã hội
Mạng xã hội  Lập trình
Lập trình  Giáo dục - Học tập
Giáo dục - Học tập  Lối sống
Lối sống  Tài chính & Mua sắm
Tài chính & Mua sắm  AI Trí tuệ nhân tạo
AI Trí tuệ nhân tạo  ChatGPT
ChatGPT  Gemini
Gemini  Prompt
Prompt  Điện máy
Điện máy  Tivi
Tivi  Tủ lạnh
Tủ lạnh  Điều hòa
Điều hòa  Máy giặt
Máy giặt  Cuộc sống
Cuộc sống  TOP
TOP  Kỹ năng
Kỹ năng  Món ngon mỗi ngày
Món ngon mỗi ngày  Nuôi dạy con
Nuôi dạy con  Mẹo vặt
Mẹo vặt  Phim ảnh, Truyện
Phim ảnh, Truyện  Làm đẹp
Làm đẹp  DIY - Handmade
DIY - Handmade  Du lịch
Du lịch  Quà tặng
Quà tặng  Giải trí
Giải trí  Là gì?
Là gì?  Nhà đẹp
Nhà đẹp  Giáng sinh - Noel
Giáng sinh - Noel  Ô tô, Xe máy
Ô tô, Xe máy  Tấn công mạng
Tấn công mạng  Chuyện công nghệ
Chuyện công nghệ  Công nghệ mới
Công nghệ mới  Trí tuệ Thiên tài
Trí tuệ Thiên tài