Cấu trúc dữ liệu ngăn xếp (Stack)

Ngăn xếp (Stack) là gì?

Một ngăn xếp là một cấu trúc dữ liệu trừu tượng (Abstract Data Type – viết tắt là ADT), hầu như được sử dụng trong hầu hết mọi ngôn ngữ lập trình. Đặt tên là ngăn xếp bởi vì nó hoạt động như một ngăn xếp trong đời sống thực, ví dụ như một cỗ bài hay một chồng đĩa...

Trong đời sống thực, ngăn xếp chỉ cho phép các hoạt động tại vị trí trên cùng của ngăn xếp. Ví dụ, chúng ta chỉ có thể đặt hoặc thêm một lá bài hay một cái đĩa vào trên cùng của ngăn xếp. Do đó, cấu trúc dữ liệu trừu tượng ngăn xếp chỉ cho phép các thao tác dữ liệu tại vị trí trên cùng. Tại bất cứ thời điểm nào, chúng ta chỉ có thể truy cập phần tử trên cùng của ngăn xếp.

Đặc điểm này làm cho ngăn xếp trở thành cấu trúc dữ liệu dạng LIFO. LIFO là viết tắt của Last-In-First-Out. Ở đây, phần tử được đặt vào (được chèn, được thêm vào) cuối cùng sẽ được truy cập đầu tiên. Trong thuật ngữ ngăn xếp, hoạt động chèn được gọi là hoạt động PUSH và hoạt động xóa được gọi là hoạt động POP.

Biểu diễn cấu trúc dữ liệu ngăn xếp (Stack)

Dưới đây là sơ đồ minh họa một ngăn xếp và các hoạt động diễn ra trên ngăn xếp.

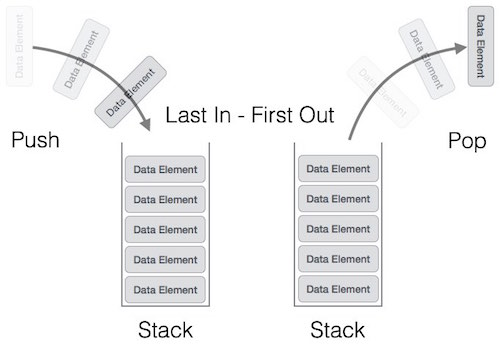
Một ngăn xếp có thể được triển khai theo phương thức của Mảng (Array), Cấu trúc (Struct), Con trỏ (Pointer) và Danh sách liên kết (Linked List). Ngăn xếp có thể là ở dạng kích cỡ cố định hoặc ngăn xếp có thể thay đổi kích cỡ. Phần dưới chúng ta sẽ triển khai ngăn xếp bởi sử dụng các mảng với việc triển khai các ngăn xếp cố định.

Các hoạt động cơ bản trên cấu trúc dữ liệu ngăn xếp

Các hoạt động cơ bản trên ngăn xếp có thể liên quan tới việc khởi tạo ngăn xếp, sử dụng nó và sau đó xóa nó. Ngoài các hoạt động cơ bản này, một ngăn xếp có hai hoạt động nguyên sơ liên quan tới khái niệm, đó là:

Hoạt động push(): lưu giữ một phần tử trên ngăn xếp.

Hoạt động pop(): xóa một phần tử từ ngăn xếp.

Khi dữ liệu đã được PUSH lên trên ngăn xếp:

Để sử dụng ngăn xếp một cách hiệu quả, chúng ta cũng cần kiểm tra trạng thái của ngăn xếp. Để phục vụ cho mục đích này, dưới đây là một số tính năng hỗ trợ khác của ngăn xếp:

Hoạt động peek(): lấy phần tử dữ liệu ở trên cùng của ngăn xếp, mà không xóa phần tử này.

Hoạt động isFull(): kiểm tra xem ngăn xếp đã đầy hay chưa.

Hoạt động isEmpty(): kiểm tra xem ngăn xếp là trống hay không.

Tại mọi thời điểm, chúng ta duy trì một con trỏ tới phần tử dữ liệu vừa được PUSH cuối cùng vào trên ngăn xếp. Vì con trỏ này luôn biểu diễn vị trí trên cùng của ngăn xếp vì thế được đặt tên là top. Con trỏ top cung cấp cho chúng ta giá trị của phần tử trên cùng của ngăn xếp mà không cần phải thực hiện hoạt động xóa ở trên (hoạt động pop).

Phần tiếp theo chúng ta sẽ tìm hiểu về các phương thức để hỗ trợ các tính năng của ngăn xếp.

Phương thức peek() của cấu trúc dữ liệu ngăn xếp

Giải thuật của hàm peek():

Bắt đầu hàm peek

   return stack[top]
   
kết thúc hàm

Sự triển khai của hàm peek() trong ngôn ngữ C:

int peek() {
   return stack[top];
}

Phương thức isFull() của cấu trúc dữ liệu ngăn xếp

Giải thuật của hàm isFull():

Bắt đầu hàm isfull

   if top bằng MAXSIZE
      return true
   else
      return false
   kết thúc if
   
kết thúc hàm

Sự triển khai của hàm isFull() trong ngôn ngữ C:

bool isfull() {
   if(top == MAXSIZE)
      return true;
   else
      return false;
}

Phương thức isEmpty() của cấu trúc dữ liệu ngăn xếp

Giải thuật của hàm isEmpty():

bắt đầu hàm isempty

   if top nhỏ hơn 1
      return true
   else
      return false
   kết thúc if
   
kết thúc hàm

Sự triển khai của hàm isEmpty() trong ngôn ngữ C khác hơn một chút. Chúng ta khởi tạo top tại -1, giống như chỉ mục của mảng bắt đầu từ 0. Vì thế chúng ta kiểm tra nếu top là dưới 0 hoặc -1 thì ngăn xếp là trống. Dưới đây là phần code:

bool isempty() {
   if(top == -1)
      return true;
   else
      return false;
}

Hoạt động PUSH trong cấu trúc dữ liệu ngăn xếp

Tiến trình đặt (thêm) một phần tử dữ liệu mới vào trên ngăn xếp còn được biết đến với tên Hoạt động PUSH. Hoạt động push bao gồm các bước sau:

Bước 1: kiểm tra xem ngăn xếp đã đầy hay chưa.

Bước 2: nếu ngăn xếp là đầy, tiến trình bị lỗi và thoát ra.

Bước 3: nếu ngăn xếp chưa đầy, tăng top để trỏ tới phần bộ nhớ trống tiếp theo.

Bước 4: thêm phần tử dữ liệu vào vị trí nơi mà top đang trỏ đến trên ngăn xếp.

Bước 5: trả về success.

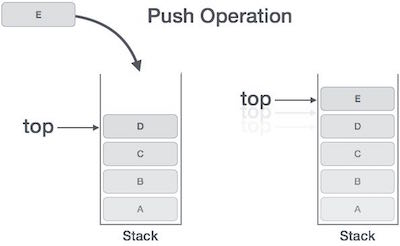
Nếu Danh sách liên kết được sử dụng để triển khai ngăn xếp, thì ở bước 3 chúng ta cần cấp phát một không gian động.

Giải thuật cho hoạt động PUSH của cấu trúc dữ liệu ngăn xếp

Từ trên có thể suy ra một giải thuật đơn giản cho hoạt động PUSH trong cấu trúc dữ liệu ngăn xếp như sau:

bắt đầu hoạt động push: stack, data

   if stack là đầy
      return null
   kết thúc if
   
   top ← top + 1
   
   stack[top] ← data

kết thúc hàm

Sự triển khai của giải thuật này trong ngôn ngữ C là:

void push(int data) {
   if(!isFull()) {
      top = top + 1;   
      stack[top] = data;
   }else {
      printf("Khong the chen them du lieu vi Stack da day.\n");
   }
}

Để tìm hiểu chương trình C minh họa đầy đủ các hoạt động trên của ngăn xếp, mời bạn vào chương: Ngăn xếp (Stack) trong C.

Hoạt động POP của cấu trúc dữ liệu ngăn xếp

Việc truy cập nội dung phần tử trong khi xóa nó từ ngăn xếp còn được gọi là Hoạt động POP. Trong sự triển khai Mảng của hoạt động pop(), phần tử dữ liệu không thực sự bị xóa, thay vào đó top sẽ bị giảm về vị trí thấp hơn trong ngăn xếp để trỏ tới giá trị tiếp theo. Nhưng trong sự triển khai Danh sách liên kết, hoạt động pop() thực sụ xóa phần tử xữ liệu và xóa nó khỏi không gian bộ nhớ.

Hoạt động POP có thể bao gồm các bước sau:

Bước 1: kiểm tra xem ngăn xếp là trống hay không.

Bước 2: nếu ngăn xếp là trống, tiến trình bị lỗi và thoát ra.

Bước 3: nếu ngăn xếp là không trống, truy cập phần tử dữ liệu tại top đang trỏ tới.

Bước 4: giảm giá trị của top đi 1.

Bước 5: trả về success.

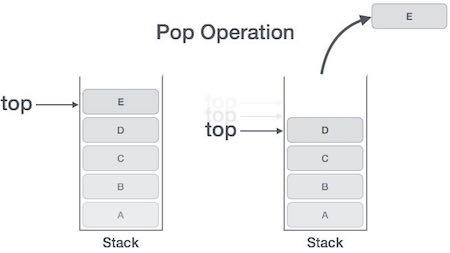
Giải thuật cho hoạt động POP

Từ trên ta có thể suy ra giải thuật cho hoạt động POP trên cấu trúc dữ liệu ngăn xếp như sau:

bắt đầu hàm pop: stack

   if stack là trống
      return null
   kết thúc if
   
   data ← stack[top]
   
   top ← top - 1
   
   return data

kết thúc hàm

Sự triển khai giải thuật trong ngôn ngữ C như sau:

int pop(int data) {

   if(!isempty()) {
      data = stack[top];
      top = top - 1;   
      return data;
   }else {
      printf("Khong the lay du lieu, Stack la trong.\n");
   }
}

Để tìm hiểu chương trình C minh họa đầy đủ các hoạt động trên của ngăn xếp, mời bạn vào chương: Ngăn xếp (Stack) trong C.

Ứng dụng của ngăn xếp

- Xử lý gọi hàm trong C/C++ - Trong máy tính, sử dụng để tính giá trị biểu thức, xử lý ngắt - Trong các chương trình biên dịch - Trong trình duyệt web, trình soạn thảo văn bản - Định giá biểu thức + Biểu thức trung tố: toán tử hai ngôi đứng giưã hai toán hạng, toán tử một ngôi đứng trước toán hạng + Biểu thức hậu tố : toán tử đứng sau toán hạng + Biểu thức tiền tố : toán tử đứng trước toán hạng

VD định giá biểu thức A = b + c * d /e – f Trung tố a*(b-c)/d Hậu tố abc-*d/ Tiền tố /*a-bcd

Duyệt biểu thức hậu tố :

- Gặp toán hạng: đẩy vào stack - Gặp toán tử 1 ngôi : lấy ra 1 toán hạng trong stack, áp dụng toán tử lên toán hạng và đấy kết quả trở lại stack - Gặp toán tử 2 ngôi :lấy 2 toán hạng ở đỉnh stack theo thứ tự, áp dụng toán tử lên 2 toán hạng đó, kết quả lại đẩy vào stack - Kết thúc, đưa ra kết quả là giá trị ở đỉnh stack - Vd định giá biểu thức hậu tố

Chuyển biểu thức dạng trung tố sang hậu tố

Duyệt lần lượt biểu thưc trung tố từ trái qua phải - Gặp toán hạng : viết sang biểu thức kết quả - Gặp toán tử có độ ưu tiên nhỏ hơn 6 + Nếu stack rỗng hoặc đỉnh stack là toán tử có độ ưu tiên nhỏ hơn hoặc là '(' đẩy toán tử đang xét vào stack + Ngược lại : lấy các toán tử ở đỉnh stack có độ ưu tiên lớn hơn hoặc bằng toán tử đang xét lần lượt đưa vào nbieeur thức kết quả và đẩy toán tử đang xét vào stack - Gặp toán tử có được ưu tiên 6 hoặc '(' thì đẩy vào stack - Gặp ')' lấy tất cả các toán tử trong stack cho đến khi gặp '(' đầu tiên, đưa sang biểu thức kết quả theo đúng thứ tự và đẩy 1 kí hiệu '(' ra khỏi stack - Nếu duyệt hết biểu thức trung tố, lấy nốt những toán tử trong stack đưa sang biểu thức kết quả theo đúng thứ tự.

Theo Tutorialspoint

Bài trước: Cấu trúc dữ liệu Danh sách liên kết vòng (Circular Linked List)

Bài tiếp: Cấu trúc dữ liệu hàng đợi (Queue)