Trọng tâm là gì? Công thức tính trọng tâm của tam giác

PP

Trọng tâm của tam giác là một trong những kiến thức rất quan trọng và phổ biến trong những năm học phổ thông. Bài viết dưới đây, Quantrimang.com xin giới thiệu với các bạn các kiến thức liên quan tới trọng tâm tam giác, công thức tính trọng tâm tam giác, công thức tính tọa độ trọng tam giác, mời các bạn tham khảo để ứng dụng vào giải các bài toán trong quá trình học tập nhé.

Mục lục bài viết

Trọng tâm là gì?
Tính chất của trọng tâm trong tam giác
Cách tìm trọng tâm tam giác
Bài tập về trọng tâm tam giác
Tọa độ của trọng tâm tam giác trong mặt phẳng Oxy

Trọng tâm là gì?

Ba đường trung tuyến của một tam giác cùng đi qua một điểm.
Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác.

Tính chất của trọng tâm trong tam giác

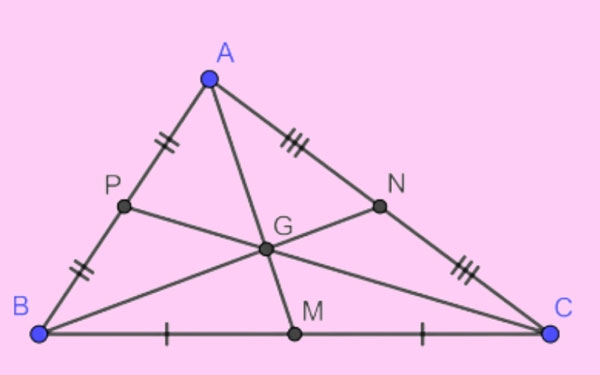
Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.

Tam giác ABC, với các đường trung tuyến AM, BN, CP và trọng tâm G, ta có:

$GA = \frac{2}{3}AM$
$GB = \frac{2}{3}BN$
$GC = \frac{2}{3}CP$

Tính chất trọng tâm của tam giác

Trọng tâm tam giác vuông

Trọng tâm của tam giác vuông cũng được xác định giống như trọng tâm của tam giác thường.

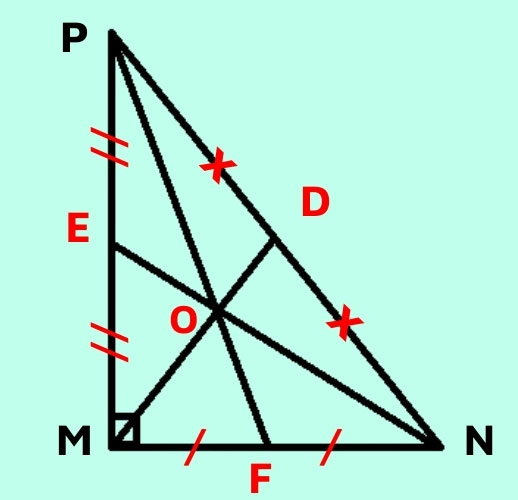
Tam giác MNP vuông tại M.

3 đường trung tuyến MD, NE, PF giao nhau tại trọng tâm O. Ta có MD là trung tuyến của góc vuông PMN nên MD = 1/2 PN = DP = DN.

Trọng tâm tam giác vuông

Trọng tâm tam giác cân

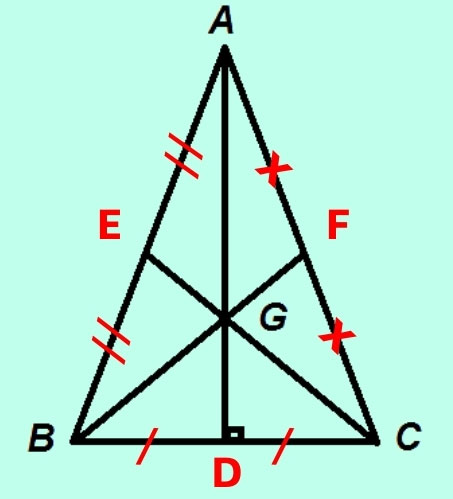
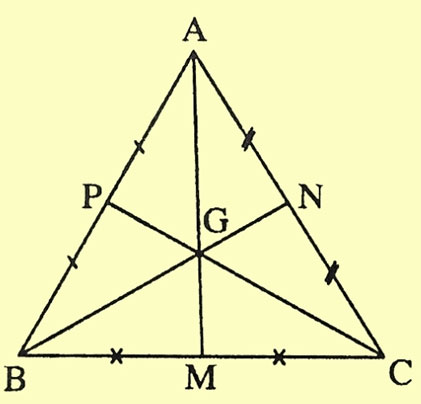
Tam giác ABC cân tại A, có G là trọng tâm.

Vì tam giác ABC cân tại A nên AG vừa là đường trung tuyến, đường cao, đường trung trực và là đường phân giác, từ đó ta suy ra được hệ quả của trọng tâm tam giác cân ABC như sau:

Góc BAD bằng góc CAD.
Trung tuyến AD vuông góc với cạnh đáy BC.

Trọng tâm tam giác cân

Trọng tâm của tam giác vuông cân

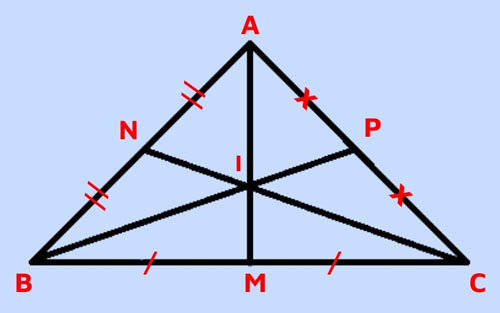
Có tam giác ABC vuông cân tại A và I là trọng tâm. AM là đường trung trực, đường trung tuyến, đường phân giác và đường cao của tam giác này nên AM vuông góc với BC.

Mặt khác, vì tam giác ABC vuông cân tại A nên:

AB = AC.

=> BP = CN và BN = AN = CP = AP.

Trọng tâm tam giác vuông cân

Trọng tâm tam giác đều

Tam giác ABC đều, G là giao điểm ba đường trung tuyến, đường cao, đường phân giác.

Vì vậy theo tính chất của tam giác đều ta có G vừa là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.

Trọng tâm tam giác đều

Cách tìm trọng tâm tam giác

Cách 1: Giao điểm 3 đường trung tuyến

Xác định trọng tâm tam giác bằng cách lấy giao điểm của ba đường trung tuyến.

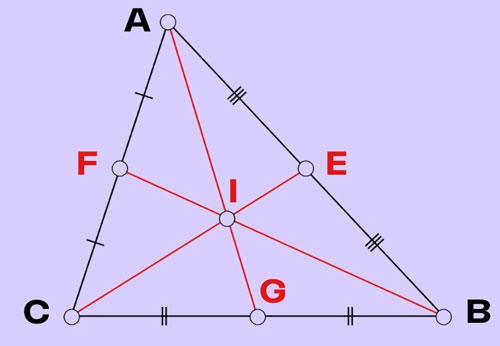
Bước 1: Vẽ tam giác ABC, lần lượt xác định trung điểm của các cạnh AB, BC, CA.

Bước 2: Nối lần lượt các đỉnh đến trung điểm của cạnh đối diện. Nối A với G, B với F, C với E.

Bước 3: Giao điểm I của ba đường trung tuyến là AG, BF, CE là trọng tâm của tam giác ABC.

Giao điểm 3 đường trung tuyến

Cách 2: Tỉ lệ trên đường trung tuyến

Xác định trọng tâm tam giác dựa trên tỉ lệ đường trung tuyến.

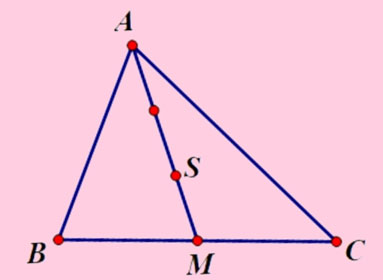
Bước 1: Vẽ tam giác ABC, xác định trung điểm M của cạnh BC.

Bước 2: Nối đỉnh A với trung điểm M, sau đó lấy điểm S sao cho AS = 2/3 AM.

Theo tính chất trọng tâm tam giác thì điểm S chính là trọng tâm tam giác ABC.

Xác định trọng tâm tam giác dựa trên tỉ lệ đường trung tuyến.

Bài tập về trọng tâm tam giác

Dạng 1: Sử dụng tính chất trọng tâm tam giác

Phương pháp giải

- Ba đường trung tuyến của tam giác đồng quy tại một điểm. Điểm này gọi là trọng tâm của tam giác.

- Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.

Bước 1. Xác định trọng tâm nằm trên đường trung tuyến nào.

Bước 2. Sử dụng linh hoạt tỉ lệ khoảng cách từ trọng tâm đến hai đầu đoạn thẳng trung tuyến.

Ví dụ 1: Cho tam giác ABC có hai đường trung tuyến BM, CN cắt nhau tại G. Chứng minh rằng: $BM + CN > \frac{3}{2}BC$ .

Hướng dẫn giải

Hình vẽ minh họa:

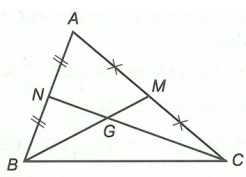
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

Xét tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G.

Suy ra G là trọng tâm tam giác ABC

$\Rightarrow BG = \frac{2}{3}BM;CG = \frac{2}{3}CN$

Do đó ta phải chứng minh $\frac{3}{2}BG + \frac{3}{2}CG > \frac{3}{2}BC$ hay $BG + CG > BC\left( 1 \right)$

Bất đẳng thức (1) luôn đúng vì trong một tam giác tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại.

Vậy $BM + CN > \frac{3}{2}BC$ , (điều phải chứng minh).

Ví dụ 2. Cho tam giác ABC. Trên cạnh BC lấy điểm G sao cho BG = 2GC. Vẽ điểm D sao cho C là trung điểm của AD. Gọi E là trung điểm của BD.

Chứng minh:

a) Ba điểm A, G, E thẳng hàng.

b) Đường thẳng DG đi qua trung điểm của AB.

Hướng dẫn giải

Hình vẽ minh họa

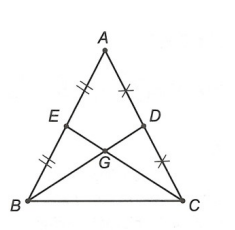
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

a) Xét tam giác ABD có C là trung điểm của cạnh AD

=> BC là trung tuyến của tam giác ABD.

Hơn nữa G ∈ BC và GB = 2GC

=> $GB = \frac{2}{3}BC$

=> G là trọng tâm tam giác ABD.

Lại có AE là đường trung tuyến của tam giác ABD nên A, G, E thẳng hàng.

b) Ta có G là trọng tâm tam giác ABD

=> DG là đường trung tuyến của tam giác này.

Suy ra DG đi qua trung điểm của cạnh AB (điều phải chứng minh).

Dạng 2: Chứng minh một điểm là trọng tâm tam giác

Phương pháp giải

Sử dụng tính chất trọng tâm. Chẳng hạn để chứng minh G là trọng tâm tam giác ABC, có ba đường trung tuyến AD, BE, CF thì ta chứng minh:

Cách 1.

$G \in AD;GA = \frac{2}{3}AD$

Hoặc $G \in BE;GB = \frac{2}{3}BE$

Hoặc $G \in CF;GC = \frac{2}{3}CF$

Cách 2.

Chứng minh G là giao điểm của hai trong ba đường trung tuyến của tam giác ABC.

Ví dụ 1: Cho tam giác ABC có đường trung tuyến AD, trên đoạn thẳng AD lấy hai điểm E, G sao cho AE = EG = GD. Chứng minh G là trọng tâm tam giác ABC.

Hướng dẫn giải

Hình vẽ minh họa

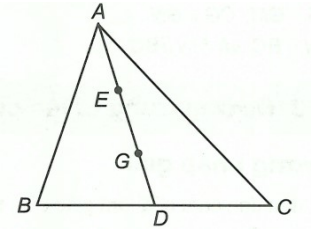
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

Ta có AD = AE + EG + GD mà AE = EG = GD nên AD = 3AE

$\Rightarrow AE = EG = GD = \frac{1}{2}AD \Rightarrow AG = \frac{2}{3}AD$

Vì AD là đường trung tuyến và $AG = \frac{2}{3}AD$ nên G là trọng tâm tam giác ABC.

Ví dụ 2: Cho tam giác ABC, D là trung điểm của AC. Trên đoạn BD lấy điểm E sao cho BE = 2ED. Điểm F thuộc tia đối của tia DE sao cho BF = 2BE. Gọi K là trung điểm của CF và G là giao điểm của EK với AC.

a) Chứng minh G là trọng tâm tam giác EFC.

b) Tính các tỉ số $\frac{{GE}}{{GK}};\frac{{GC}}{{DC}}$

Hướng dẫn giải

Hình vẽ minh họa

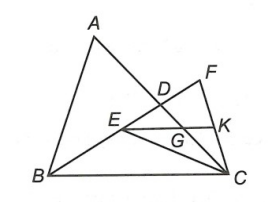
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

a) Ta có BF = 2BE; BE = EF

Mà BE = 2ED nên EF = 2ED

=> D là trung điểm của EF

=> CD là đường trung tuyến của tam giác EFC.

Vì K là trung điểm của CF nên EK là đường trung tuyến của tam giác EFC.

Tam giác EFC có hai đường trung tuyến CD và EK cắt nhau tại G nên G là trọng tâm của tam giác EFC.

b) Ta có G là trọng tâm tam giác EFC nên $\frac{{GC}}{{DC}} = \frac{2}{3};GE = \frac{2}{3}EK$

$\Rightarrow GK = \frac{1}{3}EK \Rightarrow GE = 2GK \Rightarrow \frac{{GE}}{{GK}} = 2$

Dạng 3. Đường trung tuyến của tam giác cân, tam giác đều, tam giác vuông

Phương pháp giải

Chú ý đến tính chất của tam giác cân, tam giác đều và tam giác vuông.

Ví dụ: Cho tam giác đều ABC có ba đường trung tuyến AD, BE, CF cắt nhau tại G.

Chứng minh:

a) AD = BE = CF.

b) GA = GB = GC.

Hướng dẫn giải

Hình vẽ minh họa

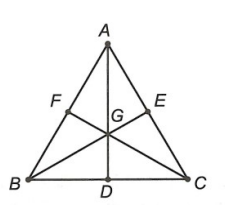
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

a) Ta có BE; CF là các đường trung tuyến của tam giác ABC

=> $CE = \frac{1}{2}AC;BF = \frac{1}{2}AB$

Vì AC = AB nên $\frac{1}{2}AC = \frac{1}{2}AB$ hay CE = BF.

Xét tam giác BCE và tam giác CBF có

BC chung; $\widehat {BCE} = \widehat {CBF}$ (do tam giác ABC cân ở A); CE = BF (chứng minh trên).

Do đó ∆BCE = ∆CBF (c.g.c)

=> BE = CF (2 cạnh tương ứng).

Chứng minh tương tự ta có AD = BE.

Từ đó suy ra AD = BE = CF (điều phải chứng minh).

b) Vì G là trọng tâm tam giác ABC nên $AG = \frac{2}{3}AD;BG = \frac{2}{3}BE;CG = \frac{2}{3}CF$

Vì AD = BE = CF (theo chứng minh câu a) nên $\frac{2}{3}AD = \frac{2}{3}BE = \frac{2}{3}CF$ hay GA = GB = GC (điều phải chứng minh)

Bài 1:

Tam giác ABC có trung tuyến AD = 9cm và trọng tâm I. Tính độ dài đoạn AI?

Giải:

Ta có I là trọng tâm của tam giác ABC và AD là đường trung tuyến nên AI = (2/3) AD (theo tính chất ba đường trung tuyến của tam giác).

Do đó: AG = (2/3).9 = 6 (cm).

Vậy đoạn AI có độ dài 6 cm.

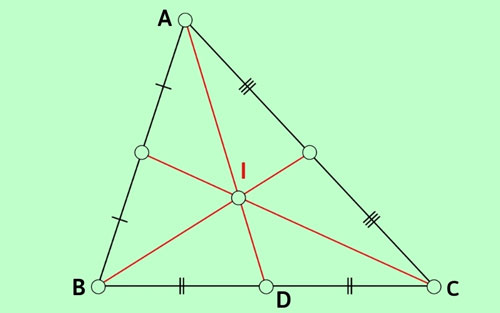
Tam giác ABC có trung tuyến AD = 9cm và trọng tâm I

Bài 2:

Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng: IM = IN = IP.

Giải:

Gọi trung điểm MN, MP, PN lần lượt là R, O, S.

Khi đó MS, PR, NO đồng quy tại trọng tâm I.

Ta có ∆MNP đều, suy ra:

MS = PR = NO (1).

Vì I là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:

MI = 2/3 MS, PI = 2/3 PR, NI = 2/3 NO (2).

Từ (1) , (2) ⇒ GA = GB = GC.

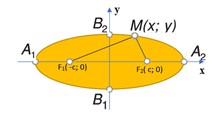
Tọa độ của trọng tâm tam giác trong mặt phẳng Oxy

Cho tam giác ABC có A(xA; yA), B(xB; yB), C(xC; yC). Nếu G là trọng tâm của tam giác ABC thì:

$\left\{\begin{array}{l}x_G=\frac{x_A+x_B+x_C}{3} \\ y_G=\frac{y_A+y_B+y_C}{3}\end{array}\right.$

Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho các điểm A(2; 0), B(0; 4), C(1; 3).

a, Chứng minh rằng A, B, C là 3 đỉnh của một tam giác.

b, Tìm tọa độ trong tâm tam giác ABC.

Hướng dẫn giải:

a, Ta có: =(-2; 4) và =(-1; 3)

Do $\frac{-2}{-1}\ne\frac{4}{3}$ nên $\overrightarrow{AB},\overrightarrow{\ AC}$ không cùng phương, suy ra A, B, C không thẳng hàng.

Vậy A, B, C là 3 đỉnh của một tam giác.

b, Gọi G là trọng tâm tam giác ABC. Suy ra tọa độ của G là:

$\left\{\begin{array}{l} x_G=\frac{x_A+x_B+x_C}{3}=\frac{2+0+1}{3}=1 \\ y_G=\frac{y_A+y_B+y_C}{3}=\frac{0+4+3}{3}=\frac{7}{3} \end{array}\right.$

Vậy tọa độ trọng tâm tam giác ABC là G (1; $\frac{7}{3}$ ).

Ngoài khái niệm và các công thức về trọng tâm tam giác ở trên, các bạn có thể tìm hiểu thêm các kiến thức khác về tam giác như diện tích tam giác, chu vi tam giác, đường cao tam giác.

Thứ Tư, 04/12/2024 09:19

3,4 ★ 39 👨 345.560