Công thức lượng giác đầy đủ nhất cho lớp 9, lớp 10, lớp 11

PP

Công thức sin cos là gì? Bài viết sẽ tổng hợp tất cả công thức tính lượng giác nhằm giúp các bạn tiện tìm kiếm.

Công thức lượng giác là các phương trình liên hệ các tỷ số lượng giác khác nhau với nhau. Chúng rất cần thiết để giải quyết nhiều bài toán trong toán học, vật lý, kỹ thuật và các lĩnh vực khác.

Một số công thức lượng giác phổ biến là:

Định nghĩa cơ bản: Các công thức này định nghĩa các tỷ số lượng giác (sin, cos, tan, v.v.) theo các cạnh của một tam giác vuông.
Định lý Pythagore: Định lý này liên hệ độ dài các cạnh trong một tam giác vuông.
Mối quan hệ góc: Các công thức này liên hệ các tỷ số lượng giác của các góc khác nhau, chẳng hạn như công thức tổng và hiệu, công thức góc đôi và công thức góc một nửa.
Đồng nhất thức nghịch đảo: Các công thức này biểu thị một tỷ số lượng giác theo một tỷ số lượng giác khác, chẳng hạn như sin(θ) = 1/coc(θ).
Đường tròn đơn vị: Đường tròn đơn vị là biểu diễn đồ họa của các tỷ số lượng giác và có thể được sử dụng để suy ra nhiều công thức khác.
Định luật Sin và Định luật Cosin: Các định luật này liên hệ đến các cạnh và góc của mọi tam giác, không chỉ tam giác vuông.

Bài viết tổng hợp các công thức lượng giác đầy đủ nhất dùng trong cả chương trình toán lớp 9, 10, 11, bao gồm các công thức lượng giác cơ bản, công thức nhân, biến đổi tích thành cổng, lượng giác của các cung đặc biệt, giá trị lượng giác của các góc đặc biệt, các công thức nghiệm cơ bản... Hãy nắm vững những công thức này để có thể triển khai các dạng bài tập về lượng giác. Mời các bạn tham khảo.

11 Công thức lượng giác phải nắm chắc

Khái niệm tỉ số lượng giác của một góc nhọn
Công thức lượng giác cơ bản
Công thức cộng lượng giác
Công thức các cung liên kết trên đường tròn lượng giác
Công thức nhân
Công thức hạ bậc
Công thức biến tổng thành tích
Công thức biến đổi tích thành tổng
Nghiệm phương trình lượng giác
9. Dấu của các giá trị lượng giác
Bảng giá trị lượng giác một số góc đặc biệt
Công thức lượng giác bổ sung

Khái niệm tỉ số lượng giác của một góc nhọn

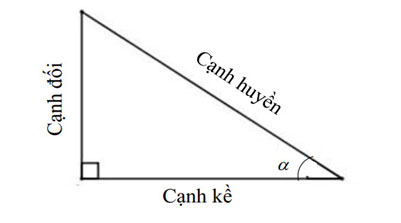
Lượng giác

Với:

sin α: là tỉ số giữa cạnh đối và cạnh huyền của góc α
cos α: là tỉ số giữa cạnh kề và cạnh huyền của góc α
tan α: là tỉ số giữa cạnh đối và cạnh kề của góc α
cot α: là tỉ số giữa cạnh kề và cạnh đối của góc α

Mẹo học thuộc : Sin đi học, Cos không hư, Tan đoàn kết, Cot kết đoàn

Công thức chuyển đổi góc sang radian và ngược lại

${\beta ^0} = \frac{{\pi .\beta }}{{{{180}^0}}}rad$

$\alpha rad = {\left( {\frac{{180\alpha }}{\pi }} \right)^0}$

Công thức lượng giác cơ bản

$1. \tan x =\frac{\sin x}{\cos x}$ với $x \neq \frac{\pi}{2} + k\pi;\left(k\mathbb{\in Z} \right)$

$2.\cot x =\frac{\cos x}{\sin x}$ với $x\neq k\pi;\left( k\mathbb{\in Z}\right)$

$3.\ \sin^2x+\cos^2x=1$

$4.\ \tan x.\cot x=1\left(x\ne k\frac{\pi}{2},\ k\ ∈\ Z\right)$

$5.\ 1+\tan^2x=\frac{1}{\cos^2x}\ \left(x\ne\frac{\pi}{2}+k\pi,\ k\ ∈\ Z\right)$

$6.\ 1+\cot^2x=\frac{1}{\sin^2x}\ \left(x\ne k\pi,\ k\ ∈\ Z\right)$

1. sin (a ± b) = sin a.cos b ± cos a.sin b

2. cos (a + b) = cos a.cos b - sin a.sin b

3. cos (a - b) = cos a.cos b + sin a.sin b

$4.\ \tan\left(a+b\right)=\frac{\tan a+\tan b}{1-\tan.\tan b}$

$5.\ \tan\left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a.\tan b}$

Mẹo nhớ công thức cộng: Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ. Tan thì tan nọ tan kia chia cho mẫu số 1 trừ tan tan.

Công thức các cung liên kết trên đường tròn lượng giác

Mẹo nhớ: cos đối, sin bù, phụ chéo, tan hơn kém π

Với mọi góc lượng giác α và số nguyên k ta có:

$\sin(\alpha + k2\pi) = \sin\alpha$
$\cos(\alpha + k2\pi) = \cos\alpha$
$\tan(\alpha + k2\pi) =\tan\alpha$
$\cot(\alpha + k2\pi) =\cot\alpha$

Hai góc đối nhau:

cos (-x) = cos x
sin (-x) = -sin x
tan (-x) = -tan x
cot (-x) = -cot x

Hai góc bù nhau:

sin (π - x) = sin x
cos (π - x) = -cos x
tan (π - x) = -tan x
cot (π - x) = -cot x

Hai góc phụ nhau:

sin (π/2 - x) = cos x
cos (π/2 - x) = sin x
tan (π/2 - x) = cot x
cot (π/2 - x) = tan x

Hai góc hơn kém π:

sin (π + x) = -sin x
cos (π + x) = -cos x
tan (π + x) = tan x
cot (π + x) = cot x

Hai góc hơn kém π/2:

sin (π/2 + x) = cos x
cos (π/2 + x) = -sin x
tan (π/2 + x) = -cot x
cot (π/2 + x) = -tan x

Công thức nhân đôi

sin2a = 2sina.cosa
cos2a = cos²a - sin²a = 2cos²a - 1 = 1 - 2sin²a
$\tan2a=\frac{2\tan a}{1-\tan^2a}$
$\cot2a=\frac{\cot^2a\ -1}{2\cot a}$

Công thức nhân ba

sin3a = 3sina - 4sin³a
cos3a = 4cos³a - 3cosa
$\tan3a=\frac{3\tan a-\tan^3a}{1-3\tan^2a}$
$\cot3a=\frac{\cot^3a-3\cot a}{3\cot^2a-1}$

Công thức nhân bốn

sin4a = 4.sina.cos³a - 4.cosa.sin³a
cos4a = 8.cos⁴a - 8.cos²a + 1 hoặc cos4a = 8.sin⁴a - 8.sin²a + 1

Công thức hạ bậc

Thực ra những công thức này đều được biến đổi ra từ công thức lượng giác cơ bản, ví dụ như: sin²a=1 - cos²a = 1 - (cos2a + 1)/2 = (1 - cos2a)/2.

$1.\ \sin^2a\ =\ \frac{1-\cos2a}{2}$

$2.\ \cos^2a=\frac{1+\cos2a}{2}$

$3.\ \sin^3a=\frac{3\sin a-\sin3a}{4}$

$4.\ \cos^3a=\frac{3\cos a+\cos3a}{4}$

Công thức biến đổi tổng thành tích

Mẹo nhớ: cos cộng cos bằng 2 cos cos, cos trừ cos bằng trừ 2 sin sin; sin cộng sin bằng 2 sin cos, sin trừ sin bằng 2 cos sin.

$1.\ \cos a+\cos b=2\cos\frac{a+b}{2}.\cos\frac{a-b}{2}$

$2.\ \cos a-\cos b=-2\sin\frac{a+b}{2}.\sin\frac{a-b}{2}$

$3.\ \sin\ a+\sin b=2\sin\frac{a+b}{2}.\cos\frac{a-b}{2}$

$4.\ \sin\ a-\sin b=2\cos\frac{a+b}{2}.\sin\frac{a-b}{2}$

$5.\ \tan a+\tan b=\frac{\sin\left(a+b\right)}{\cos a.\cos b}$

$6.\ \tan a-\tan b=\frac{\sin\left(a-b\right)}{\cos a.\cos b}$

$7.\cot a + \cot b = \frac{\sin(a +b)}{\sin a.\sin b}$

$8.\cot a - \cot b = - \frac{\sin(a -b)}{\sin a.\sin b}$

$9.\ \sin a+\cos a=\sqrt{2}\sin\left(a+\frac{\pi}{4}\right)=\sqrt{2}\cos\left(a-\frac{\pi}{4}\right)$

$10.\ \sin a-\cos a=\sqrt{2}\sin\left(x-\frac{\pi}{4}\right)=-\sqrt{2}\cos\left(x+\frac{\pi}{4}\right)$

$11.\ \tan a+\cot a=\frac{2}{\sin2a}$

$12.\ \cot a-\tan a=2\cot2a$

$13.\ \sin^4a+\cos^4a=1-\frac{1}{2}\sin^22a=\frac{1}{4}\cos4a+\frac{3}{4}$

$14.\ \sin^6a+\cos^6a=1-\frac{3}{4}\sin^22a=\frac{3}{8}\cos4a+\frac{5}{8}$

Công thức biến đổi tích thành tổng

$1.\ \cos a.\cos b=\frac{1}{2}\left[\cos\left(a+b\right)+\cos\left(a-b\right)\right]$ $2.\ \sin a.\sin b=-\frac{1}{2}\left[\cos\left(a+b\right)-\cos\left(a-b\right)\right]$

$3.\ \sin a.\cos b=-\frac{1}{2}\left[\sin\left(a+b\right)+\sin\left(a-b\right)\right]$

Phương trình lượng giác

Phương trình lượng giác cơ bản

$1.\sin a = \sin b \Leftrightarrow \left[ \begin{gathered} a = b + k2\pi \hfill \\ a = \pi - {\text{b}} + {\text{k}}2\pi \hfill \\ \end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$

$2.\cos a = \cos b \Leftrightarrow \left[ \begin{gathered} a = b + k2\pi \hfill \\ a = - b + k2\pi \hfill \\ \end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$

3. tan a = tan b ⇔ a = b + kπ; (k ∈ Z)

4. cot a = cot b ⇔ a = b + kπ; (k ∈ Z)

Phương trình lượng giác đặc biệt

sin a = 0 ⇔ a = kπ; (k ∈ Z)
sin a = 1 ⇔ a = π/2 + k2π; (k ∈ Z)
sin a = -1 ⇔ a = -π/2 + k2π; (k ∈ Z)
cos a = 0 ⇔ a = π/2 + kπ; (k ∈ Z)
cos a = 1 ⇔ a = k2π; (k ∈ Z)
cos a = -1 ⇔ a = π + k2π; (k ∈ Z)
$\tan x = 1 \Leftrightarrow x =\frac{\pi}{4} + k\pi ,(k\in \mathbb{Z})$
$\tan x = 0 \Leftrightarrow x =k\pi ,(k\in \mathbb{Z})$
$\tan x = - 1 \Leftrightarrow x = -\frac{\pi}{4} + k\pi ,(k\in \mathbb{Z})$
$\cot x = 1 \Leftrightarrow x = \frac{\pi}{4} + k\pi(k\mathbb{\in Z})$
$\cot x = 0 \Leftrightarrow x = \frac{\pi}{2} + k\pi(k\mathbb{\in Z})$

Dấu của các giá trị lượng giác

Góc phần tư số	I	II	III	IV
Giá trị lượng giác	I	II	III	IV
sin x	+	+	-	-
cos x	+	-	-	+
tan x	+	-	+	-
cot x	+	-	+	-

Bảng giá trị lượng giác một số góc đặc biệt

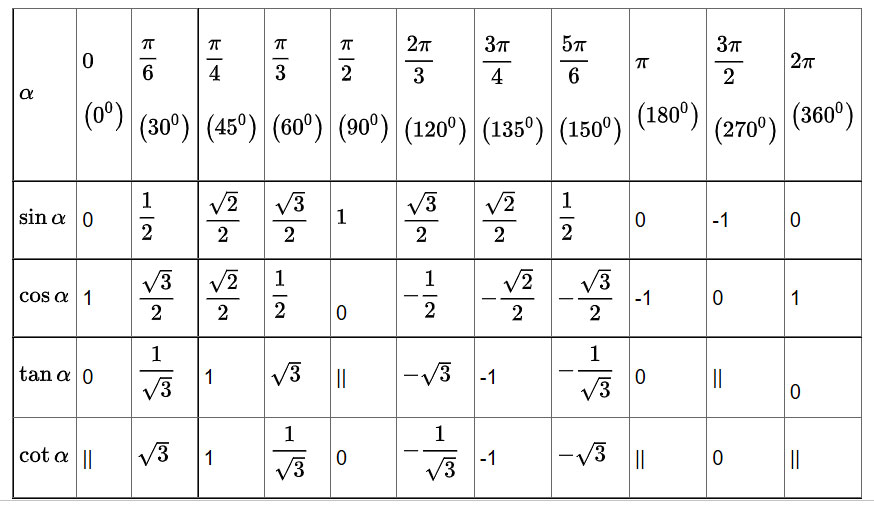
Quan sát trực quan các góc đặc biệt trên đường tròn lượng giác như sau:

Công thức lượng giác đầy đủ nhất cho lớp 9, lớp 10, lớp 11

Tỉ số lượng giác của 2 góc phụ nhau. (α + β = 90°)

sin α = cos β	cos α = sin β
tan α = cot β	cot α = tan β

Công thức lượng giác bổ sung

Biểu diễn công thức theo $t=\frac{\tan a}{2}$

$1.\ \sin a=\frac{2t}{1+t^2}\ \ \ \ \ \ \ \ \ \ \ \ 2.\ \cos a=\frac{1-t^2}{1+t^2}$

$3.\ \tan\ a=\frac{2t}{1-t^2}\ \ \ \ \ \ \ \ \ \ 4.\ \cot a=\frac{1-t^2}{2t}$

Các công thức đạo hàm và đạo hàm lượng giác đầy đủ nhất

Câu hỏi thường gặp về công thức lượng giác và các hằng đẳng thức

Lượng giác là gì?

Lượng giác là một nhánh của toán học tập trung vào mối quan hệ giữa các góc và cạnh của tam giác, đặc biệt là tam giác vuông.

Ba tỷ số lượng giác cơ bản là gì?

Sin A = Vuông góc/Cạnh huyền
Cos A = Đáy/Cạnh huyền
Tan A = Vuông góc/Cạnh đáy

Công thức lượng giác áp dụng cho tam giác nào?

Công thức lượng giác áp dụng cho tam giác vuông.

Các tỷ số lượng giác chính là gì?

Sin, Cosin, Tangent, Cotangent, Secant và Cosecant.

Đối với góc nào thì giá trị của tỷ số tan bằng tỷ số cot?

Đối với giá trị 45°, tan 45°= cot 45° = 1.

Công thức sin3x là gì?

Công thức sin3x là 3sin x – 4 sin3x.

Trên đây là tất cả những kiến thức bạn cần biết về công thức lượng giác. Bài viết bao gồm cả ví dụ cụ thể và bài tập minh họa, giúp bạn dễ học, ghi nhớ và thực hành.

Thứ Sáu, 21/03/2025 16:44

3,8 ★ 50 👨 213.777

Bạn nên đọc

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!