Công thức tính tỉ số thể tích các khối đa diện

PP

Để giải các bài toán về thể tích khối đa diện, các bạn cần nắm được công thức tính thể tích và tỉ số thể tích khối đa diện của các khối đa diện như khối chóp tam giác, khối chóp có đáy là hình bình hành… Dưới đây là công thức tính nhanh tỉ số thể tích khối chóp tam giác, công thức tính nhanh tỉ số thể tích khối chóp có đáy là hình bình hành, hai khối chóp chung chiều cao, hai khối đa diện đồng dạng tỉ số k, mời các bạn tham khảo.

Công thức tính tỉ số thể tích các khối đa diện

Công thức tính tỉ số thể tích khối chóp tam giác
Công thức tính tỉ số thể tích khối chóp có đáy là hình bình hành
Công thức tính tỉ số thể tích hai khối chóp chung chiều cao
Công thức tính tỉ số thể tích hai khối đa diện đồng dạng tỉ số k
Công thức tính nhanh tỉ số thể tích khối lăng trụ tam giác
Công thức tính nhanh tỉ số thể tích khối lăng trụ đáy là hình bình hành (khối hộp)

Công thức tính tỉ số thể tích khối chóp tam giác

Cho hình chóp S.ABC có 3 điểm A’. B’, C’ lần lượt nằm trên 3 cạnh SA, SB, SC. Khi đó, ta có công thức về tỷ số thể tích như sau:

$\frac{V_{S . A^{\prime B}{ }^{\prime} C^{\prime}}}{V_{S . A B C}}=\frac{S A^{\prime}}{S A} \cdot \frac{S B^{\prime}}{S B} \cdot \frac{S C^{\prime}}{S C}$

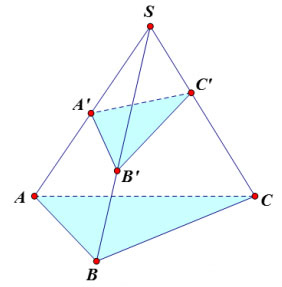
Khối chóp tam giác

Công thức trên vẫn đúng trong trường hợp A’ trùng với A. Khi đó:

$\frac{V_{S . A B^{\prime} C^{\prime}}}{V_{S . A B C}}=\frac{S A}{S A} \cdot \frac{S B^{\prime}}{S B} \cdot \frac{S C^{\prime}}{S C}$ $=\frac{S B^{\prime}}{S B} \cdot \frac{S C^{\prime}}{S C}$

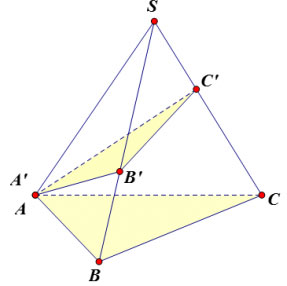
Khối chóp hình tam giác 2

ví dụ:

Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, AC=a√2; SA=a,SA⊥(ABC). Gọi G là trọng tâm của ∆SBC, một mặt phẳng (α) đi qua AG và song song với BC cắt SC, SB lần lượt taị M, N. Tính thể tích khối chóp S.AMN.

Giải:

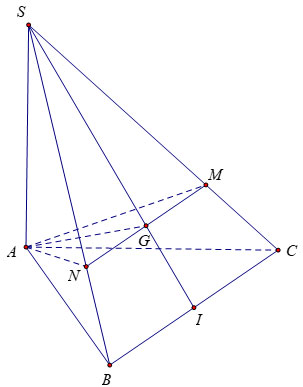
Tam giác ABC vuông tại B có AC = a√2 => AB = BC = a

Gọi I là trung điểm của BC, G là trọng tâm tam giác SBC

⇒ SG/SI = 2/3

Mà MN // BC nên ta có:

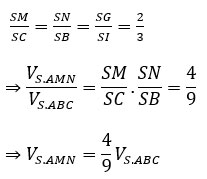
Mặt khác:

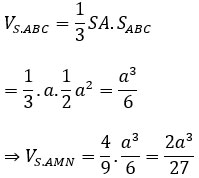
Công thức tính tỉ số thể tích khối chóp có đáy là hình bình hành

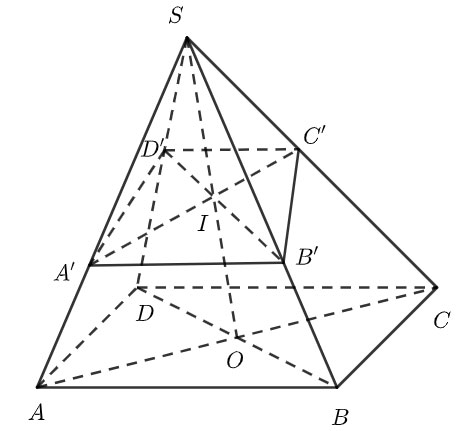
Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Trên các đoạn SA, SB, SC, SD lấy lần lượt các điểm A’, B’, C’, D’ khác S sao cho a+c=b+d. Trong đó:

$a=\frac{S A}{S A^{\prime}}$ , $b=\frac{S B}{S B^{\prime}}$ , $c=\frac{S C}{S C^{\prime}}$ , $d=\frac{S D}{S D^{\prime}}$

Khi đó ta có tỉ số thể tích là:

$\frac{V_{S \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}}{V_{S . A B C D}}=\frac{a+b+c+d}{4 a b c d}$

Khối chóp có đáy là hình bình hành

Công thức tính tỉ số thể tích hai khối chóp chung chiều cao

Nếu hai khối chóp (H) và (H’) có diện tích hai đáy lần lượt là S và S’. Đồng thời có cùng chiều cao h. Thì ta có:

$\frac{V_{H^{\prime}}}{V_H}=\frac{S^{\prime}}{S}$

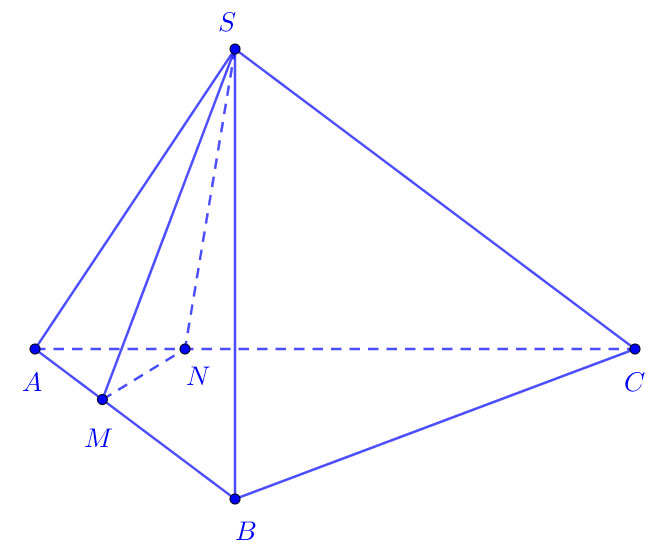
Hai khối chóp chung chiều cao

Ví dụ: Cho khối chóp S.ABC. Điểm M thuộc đoạn AB sao cho AB = 4AM. Điểm N thuộc đoạn AC sao cho AC = 3AN. Gọi V và V’ lần lượt là thể tích các khối chóp S.AMN và S.ABC. Biết V’=kV. Tìm k.

Giải:

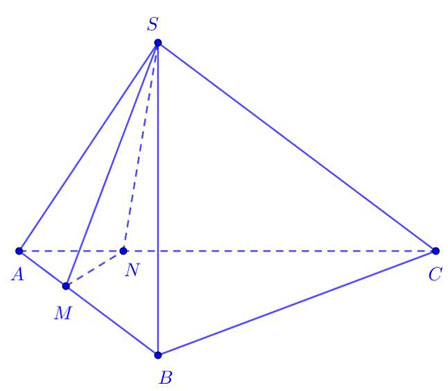
Hai khối chóp S.AMN và S.ABC chung đỉnh và chung mặt đáy nên chung chiều cao.

Do đó::

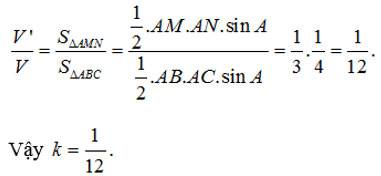
Công thức tính tỉ số thể tích hai khối đa diện đồng dạng tỉ số k

Hai khối đa diện (H) và (H’) được gọi là đồng dạng tỉ số k nếu có 1 phép đồng dạng F tỉ số k biến (H) thành (H’). Khi đó giả sử AB là 1 cạnh của (H) và F(AB)=A’B’ thì A’B’=kAB. Gọi V và V’ lần lượt là thể tích của (H) và (H’), khi đó ta có tỉ số thể tích sau:

$\frac{V^{\prime}}{V}=k^3$

Hai khối đa diện đồng dạng tỉ số k

Ví dụ:

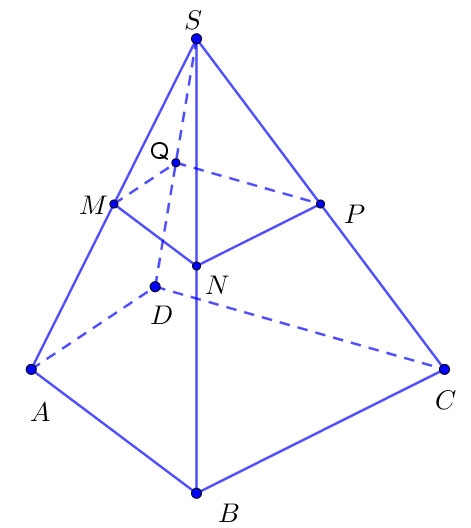
Cho khối chóp S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD. Gọi V là thể tích khối chóp S.MNPQ. Tính V biết thể tích khối chóp S.ABCD bằng 12.

Giải:

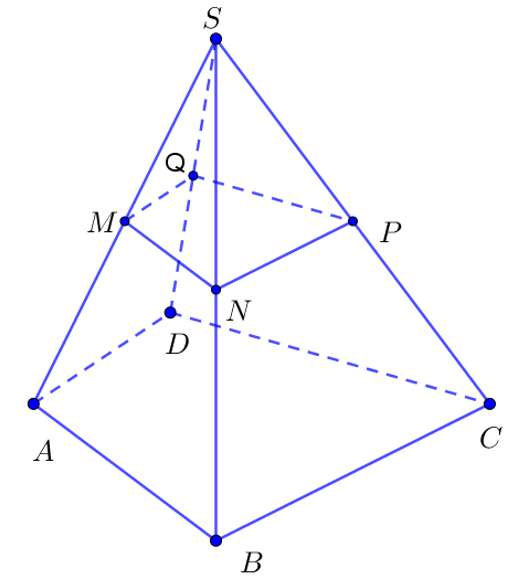
Dễ thấy phép vị tự tâm S tỉ số 2 biến khối chóp S.MNPQ thành khối chóp S.ABCD.

Do đó:

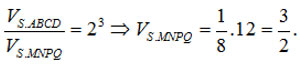
Công thức tính nhanh tỉ số thể tích khối lăng trụ tam giác

Cho khối lăng trụ tam giác ABC.A’B’C’. Trên các cạnh bên AA’, BB’, CC’ lấy lần lượt các điểm M, N, P. Khi đó ta có tỉ số sau:

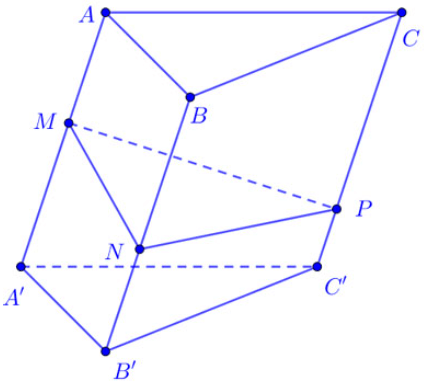
Khối lăng trụ tam giác

$\frac{V_{A B C . M N P}}{V_{A B C \cdot A^{\prime} B^{\prime} C^{\prime}}}=\frac{a+b+c}{3}$

Trong đó:

$a=\frac{A M}{A A^{\prime}}, b=\frac{B N}{B B^{\prime}}, c=\frac{C P}{C C^{\prime}}$

Công thức tính nhanh tỉ số thể tích khối lăng trụ đáy là hình bình hành (khối hộp)

Cho khối hộp ABCD.A’B’C’D’. Trên các cạnh bên AA’, BB’, CC’, DD’ lấy lần lượt các điểm M, N, P, Q sao cho M, N. P, Q đồng phẳng. Khi đó ta có tỉ số sau:

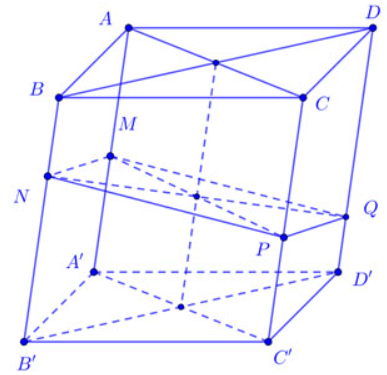
Khối lăng trụ hình bình hành

$\frac{V_{A B C D . M N P Q}}{V_{A B C D} \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}=\frac{a+b+c+d}{4}$

Trong đó:

$a=\frac{A M}{A A^{\prime}}, b=\frac{B N}{B B^{\prime}}$

$c=\frac{C P}{C C^{\prime}}, d=\frac{D Q}{D D^{\prime}}$

và a + c = b + d

Hy vọng các bạn có thể vận dụng thành thạo công thức liên quan đến tỉ số thể tích khối đa diện mà Quantrimang.com đã tổng hợp ở trên và áp dụng tốt để giải các bài toán liên quan.

Thứ Sáu, 06/12/2024 18:02

3,5 ★ 35 👨 136.797