Công thức tính diện tích hình thoi, chu vi hình thoi

Cùng ôn lại và ghi nhớ công thức tính diện tích, công thức tính chu vi hình thoi và tính đường chéo hình thoi trong bài viết dưới đây nhé.

1. Công thức tính diện tích hình thoi

Diện tích hình thoi được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình thoi.

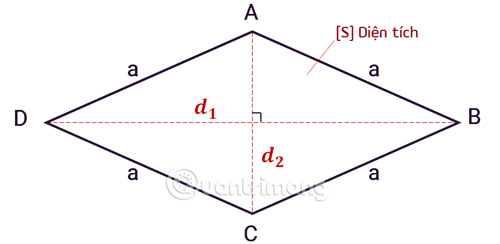
Công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao

Diện tích của hình thoi bằng một nửa tích độ dài của hai đường chéo, công thức như sau:

Trong đó:

• S là diện tích hình thoi.
• d1 và d2 là hai đường chéo của hình thoi.

Ví dụ tính diện tích hình thoi.

Bài 1: Có một tấm bìa hình thoi đo được hai đường chéo cắt nhau có chiều dài lần lượt là 6 cm và 8 cm. Hỏi diện tích của tấm bìa hình thoi đó bằng bao nhiêu?

Áp dụng theo cách tính diện tích hình thoi, ta có d1 = 6 cm và d2 = 8 cm. Ta đưa vào công thức và có kết quả như sau:

S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2

Công thức tính diện tích hình thoi dựa vào hệ thức trong tam giác (Nếu biết góc của hình thoi)

Trong đó: a: cạnh hình thoi

Ví dụ 1: Cho hình thoi ABCD, có cạnh hình thoi = 4cm, góc A = 35 độ. Tính diện tích hình thoi ABCD.

Giải: Áp dụng công thức, ta có a = 4, góc = 35 độ. Ta thay vào công thức như sau:

S = a2 x sinA = 42 x sin(35) = 9,176 (cm2)

2. Công thức tính chu vi hình thoi

Chu vi hình thoi được tính bằng tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích.

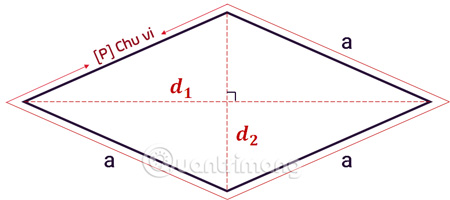
Để tính chu vi hình thoi, ta tính tổng độ dài của 4 cạnh. Công thức cụ thể như sau:

Trong đó:

• P là chu vi hình thoi.
• a là chiều dài của cạnh hình thoi.

Ví dụ: Cho một hình thoi ABCD có độ dài các cạnh bằng nhau và bằng 7 cm. Hỏi chu vi của hình thoi này bằng bao nhiêu?

Theo công thức tính chu vi hình thoi được giới thiệu ở trên, ta có a = 7 cm. Như vậy chu vi hình thoi ABCD sẽ được tính như sau:

P (ABCD) = a x 4 = 7 x 4 = 28 cm

3. Hình thoi là gì?

Hình thoi là một tứ giác có 4 cạnh bằng nhau. Đây là hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau.

Tính chất của hình thoi

• 2 góc đối bằng nhau
• 2 đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
• 2 đường chéo là các đường phân giác của các góc.

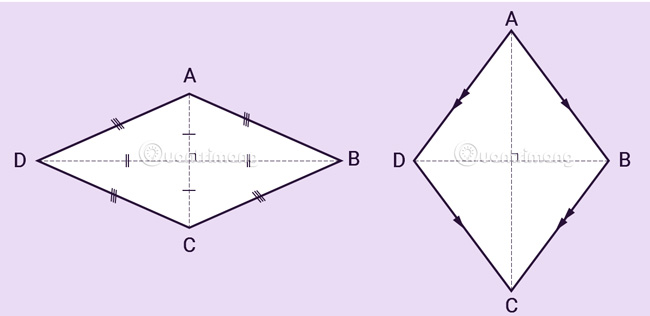
Ở bài viết này, Quantrimang.com sẽ giới thiệu lại các công thức tính diện tích và chu vi hình thoi hiệu quả cho việc học và công việc của bạn.

4. Ví dụ về tính diện tích và chu vi hình thoi

Ví dụ 1: 

Cho hình thoi ABCD có cạnh AD = 4m, có góc DAB = 30 độ. Tính diện tích của hình thoi ABCD.

Giải:

Do ABCD là hình thoi nên các tam giác tạo thành là tam giác cân, gọi I là trung điểm hai đường chéo nên AI vuông góc với BD, góc IAB = 15 độ.

Do đó, AI = AB. cos IAB = 4. Cos 15 = 3,84m.

Xét tam giác vuông ABI, theo định lý Pytago, ta có:

BI2= AB2- AI2= 1,25m

Nên BI = 1,1m

AC = 2. AI = 7,68m

BD = 2. BI = 2,2m

Dựa vào công thức tính diện tích hình thoi, ta có diện tích của hình thoi ABCD = ½ . AC . BD = 8,45(m2)

Ví dụ 2: Cho hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 60°, hãy tính diện tích hình thoi.

Với những dữ kiện này bạn sẽ chưa có cơ sở gì để tính diện tích hình thoi. Bạn sẽ phải dựa vào tính chất hình thoi, tính chất tam giác đều, cách tính các cạnh trong một tam giác vuông để tính được đường chéo của hình thoi. Các bước làm như sau:

Bước 1: Vẽ hình và ghi chú các dữ kiện đã biết.

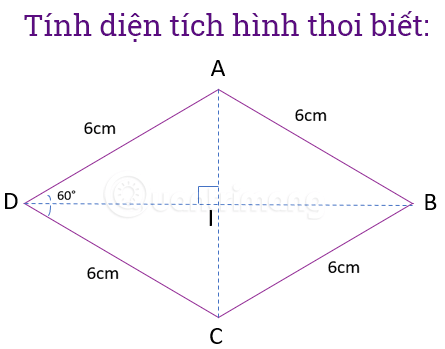
Bước 2: Vận dụng các tính chất của hình thoi ta có:

, đường chéo AC là phân giác của góc A, nên góc sẽ bằng 1/2 góc  và bằng 60°. (Tổng các góc trong của tứ giác bằng 360°, tổng các góc trong của tam giác là 180°). Như vậy, tam giác ADC sẽ là tam giác đều => cạnh AC bằng 6cm. I là trung điểm AC => AI=3cm.

Bước 3: Tính độ dài DI

Tam giác DIA vuông tại I, cạnh DI sẽ tính như sau:

=> cm

Bước 4: Tính diện tích hình thoi ABCD:

Ví dụ 3: Cho hình thoi ABCD có cạnh bằng 13cm, hai đường chéo cắt nhau tại H.

Tính diện tích hình thoi ABCD biết BH gấp rưỡi AH.

Lời giải:

ABCD là hình thoi, nên AH vuông góc với BH tại H, khi đó tam giác ABH vuông tại H.

Đặt BH= 2a, khi đó AH =3a.

Theo định lí Pytago ta có: AH²+ BH²= AB² ⇒9a²+4a²=13 ⇒13a²=13 ⇒a=1

Do đó AH= 3cm, BH= 2cm hay AC=6 cm, BD= 4cm

Diện tích hình thoi là: S = 6.4/2= 12cm².

Ví dụ 4:

Cho hinh thoi MNPQ biết góc A = 30o, chu vi = 20m, trung điểm của đường chéo là I. Hỏi diện tích hình thoi MNPQ bằng bao nhiêu?

Lời giải

Độ dài cạnh của hình thoi là a = P : 4 = 20 : 4 = 5m

Bởi hình các tam giác được tạo bởi hình thoi đều là tam giác cân nên tam giác tạo tành từ trung điểm của đường chéo I, điểm M, N sẽ được tạo bởi góc IMN = 15o

Độ dài nửa đường chéo MI = MN x cos IMN = 5 x cos150 = 4,8m

Áp dụng định lý pytago trong tam giác vuông MNI ta có: NI = 1,4m

Độ dài đường chéo NQ = 2 x NI = 2 x 1,4 = 2,8m

Diện tích hình thoi MNPQ là S = 2 x ½ x NQ x MI = 1 x ½ x 2,8 x 4,8 = 13,44m2

Đáp số: 13,44m2

Nếu có thắc mắc gì liên quan đến công thức tính diện tích và chu vi hình thoi, hãy để lại comment bên dưới để cùng nhau trao đổi và giải đáp nhé. Cảm ơn các bạn đã theo dõi bài viết.