Diện tích hình trụ: Diện tích xung quanh hình trụ, diện tích toàn phần hình trụ

Thanh Huyen

Cùng tìm hiểu về công thức tính diện tích xung quanh, diện tích toàn phần và chiều cao của hình trụ để áp dụng trong học tập và đời sống hàng ngày nhé.

Mục lục bài viết

Cách tính diện tích hình trụ
- Công thức tính diện tích xung quanh hình trụ
- Công thức tính diện tích toàn phần hình trụ
Tính chiều cao hình trụ
Công thức tính bán kính đáy của hình trụ
Hình trụ tròn là gì
Công thức tính diện tích thiết diện của hình trụ
Ví dụ tính diện tích hình trụ

Cách tính diện tích hình trụ

Diện tích hình trụ gồm có diện tích xung quanh và diện tích toàn phần.

Các bạn có thể nhập kích thước chiều cao, bán kính của hình trụ vào bảng dưới đây biết diện tích xung quanh và diện tích toàn phần của hình trụ.

Công thức tính diện tích xung quanh hình trụ

Diện tích xung quanh hình trụ chỉ bao gồm diện tích mặt xung quanh, bao quanh hình trụ, không gồm diện tích hai đáy.

Công thức tính diện tích xung quanh hình trụ bằng chu vi đường tròn đáy nhân với chiều cao.

$S_{xung quanh}=2\pi .r.h$

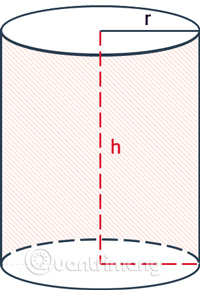Trong đó:

S_{xung quanh}là diện tích xung quanh.
r là bán kính hình trụ.
h là chiều cao, khoảng cách giữa 2 đáy của hình trụ.

Ví dụ: 1

Một hình trụ tròn có bán kính đáy r = 5 cm, chiều cao h = 7cm. Tính diện tích xung quanh hình trụ đứng.

Giải: Diện tích xung quanh của hình trụ tròn: Sxq = 2.π.r.h = 2π.5.7 = 70π = 219,8 (cm²).

Ví dụ: 2

Cho hình vuông ABCD cạnh 2a. Gọi O và O’ lần lượt là trung điểm các cạnh AB và CD. Khi quay hình vuông đó xung quanh trục OO’ ta được một hình trụ tròn xoay. Tính diện tích xung quanh hình trụ tròn xoay đó.

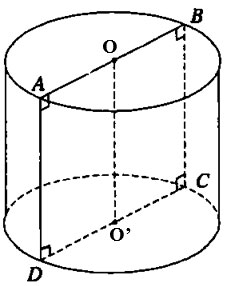
Tính diện tích hình trụ

Lời giải:

Bán kính đường tròn đáy là r= CD= a

Chiều cao hình trụ là h= OO'= AD=2a

Vậy diện tích xung quanh hình trụ là Sxq = 2πrh = 2π.a.2a =4a2π

Công thức tính diện tích toàn phần hình trụ

Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích hai đáy tròn.

Công thức tính diện tích toàn phần hình trụ bằng diện tích xung quanh cộng với diện tích của 2 đáy.

$S_{toan phan} =S_{xung quanh}+S_{2 day}$

$S_{toan phan}=2\pi .r.h +2\pi .r^{2}$

$S_{toan phan}=2\pi .r.(r+h )$

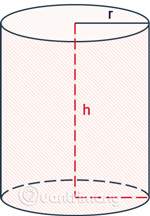Ví dụ 1: Tính diện tích toàn phần của hình trụ có đáy bằng 3 và chiều cao bằng 5.

Lời giải:

Diện tích toàn phần là Stp= Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π

Tính chiều cao hình trụ

Chiều cao hình trụ chính là khoảng cách giữa hai mặt đáy của hình trụ.

Tính chiều cao hình trụ khi biết diện tích toàn phần và bán kính đáy

$h=\frac{\text { Stoan phan }-2 \pi r^2}{2 \pi r}$

Ví dụ: Cho hình trụ có bán kính đáy R = 8cm và diện tích toàn phần 564π cm2 . Tính chiều cao của hình trụ.

Giải:

Ta có $h=\frac{564 \pi-2 \pi 8^2}{2 \pi 8}=\frac{564 \pi-128 \pi}{16 \pi}$ $=\frac{436 \pi}{16 \pi}=27,25 \mathrm{~cm}$

Tính chiều cao hình trụ khi biết diện tích xung quanh

$S_{xung quanh}=2\pi .r.h$

=> $h=\frac{Sxq}{2\pi r}$

Công thức tính bán kính đáy của hình trụ

1. Công thức tính chu vi đường tròn; diện tích hình tròn

Đường tròn có chu vi C=2πr

=> $r=\frac{C}{2 \pi}$

Hình tròn đáy có diện tích S=πr²

=> $r=\sqrt{\frac{S}{\pi}}$

Ví dụ. Tính bán kính đáy của hình trụ trong các trường hợp sau:

a. Chu vi đường tròn đáy là 6π

b. Diện tích đáy là 25π

Lời giải:

a. Bán kính đường tròn đáy là

$r=\frac{C}{2 \pi}=\frac{6 \pi}{2 \pi}=3$

b. Bán kính đường tròn đáy là

$\mathrm{r}=\sqrt{\frac{\mathrm{S}}{\pi}}=\sqrt{\frac{25 \pi}{\pi}}=5$

2. Đáy là đường tròn nội tiếp đa giác

- Nội tiếp tam giác bất kì: $\mathrm{R}=\frac{\mathrm{S}}{\mathrm{p}}$ với S là diện tích tam giác và p là nửa chu vi

- Nội tiếp tam giác đều: $R=\frac{\sqrt{3}}{6}$ cạnh

- Nội tiếp hình vuông: $\mathrm{R}=\frac{\text { cạnh }}{2}$

Ví dụ 1. Cho hình trụ nội tiếp trong một hình lập phương có cạnh a. Tính bán kính của hình trụ đó.

Bán kính hình trụ là: $R=\frac{a}{2}$

Ví dụ 2. Cho lăng trụ đều ABC.A’B’C’ có , thể tích ngoại tiếp khối trụ. Tính bán kính khối trụ đó.

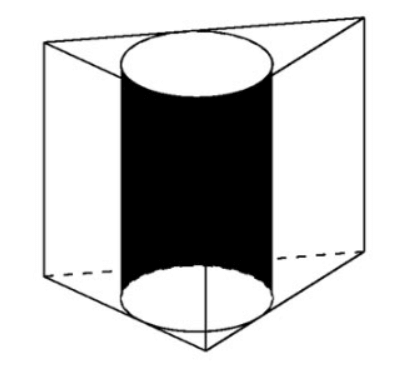
Hình trụ

Thể tích khối lăng trụ là $\mathrm{V}=\mathrm{h} \cdot \mathrm{S}_{\mathrm{d}} \Leftrightarrow=\frac{\mathrm{a}^3 \sqrt{3}}{2}$ $=\mathrm{a} \cdot \mathrm{S}_{\mathrm{d}} \Rightarrow>\mathrm{S}_{\mathrm{d}}=\frac{\mathrm{a}^2 \sqrt{3}}{2}$

Đáy lăng trụ đều là tam giác đều nên $\mathrm{S}_{\mathrm{d}}=\operatorname{cạnh}^2 \frac{\sqrt{3}}{4}$ => cạnh $=\mathrm{a} \sqrt{2}$

Do vậy bán kính đáy hình trụ là: $\mathrm{R}=\frac{\mathrm{a} \sqrt{2} \cdot \sqrt{3}}{6}=\frac{\mathrm{a}}{\sqrt{6}}$

3. Đáy là đường tròn ngoại tiếp đa giác

Ngoại tiếp tam giác bất kì: $\mathrm{R}=\frac{\mathrm{abc}}{4 \mathrm{~S}}=\frac{\mathrm{abc}}{4 \sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}}$

Trong đó:

a, b, c là độ dài 3 cạnh tam giác
p là nửa chu vi tam giác: $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$

Ngoại tiếp tam giác vuông: $\mathrm{R}=\frac{1}{2}$ cạnh huyền

Ngoại tiếp tam giác đều: $R=\frac{\sqrt{3}}{3}$ cạnh

Ngoại tiếp hinh vuông: $R=\frac{\sqrt{2}}{2}$ cạnh

Ví dụ:

Tính bán kính đáy của khối trụ ngoại tiếp khối chóp đều S.ABC trong các trường hợp sau:

a. ABC là tam giác vuông tại A có AB = a và AC = a√3

b. ABC có AB= 5; AC= 7; BC=8

Giải:

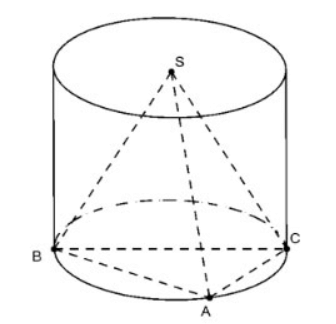
Khối trụ ngoại tiếp khối chóp đều

a. Cạnh huyền $\mathrm{BC}=\sqrt{\mathrm{AB}^2+\mathrm{AC}^2}$ $=\sqrt{\mathrm{a}^2+3 \mathrm{a}^2}=2 \mathrm{a}$

Do ABC vuông tại A nên bán kính R=0,5.BC=a

b. Nửa chu vi tam giác ABC là ${p}=\frac{5+7+8}{2}=10$
$\Rightarrow \mathrm{S}=\sqrt{10 .(10-5)(10-7)(10-8)}=10 \sqrt{3}$
$\Rightarrow \mathrm{R}=\frac{\mathrm{abc}}{4 \mathrm{~S}}=\frac{5.7 .8}{40 \sqrt{3}}=\frac{7 \sqrt{3}}{3}$

Hình trụ tròn là gì

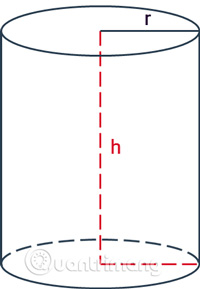
Hình trụ tròn là hình trụ có 2 đáy là hình tròn bằng nhau và song song với nhau.

Hình trụ được sử dụng khá phổ biến trong các bài toán hình học từ căn bản đến phức tạp, trong đó công thức tính diện tích, thể tích hình trụ thường được sử dụng khác phổ biến. Nếu bạn đã biết cách tính diện tích và chu vi hình tròn thì cũng có thể dễ dàng suy luận ra các công thức tính thể tích, diện tích xung quanh cũng như diện tích toàn phần của hình trụ.

Hình trụ là một hình khối quen thuộc trong cuộc sống

Hình trụ tròn là hình trụ có 2 đáy là hình tròn bằng nhau và song song với nhau.

Công thức tính diện tích thiết diện của hình trụ

Cắt hình trụ bởi mặt phẳng (P) qua trục

Thiết diện nhận được là một hình chữ nhật.

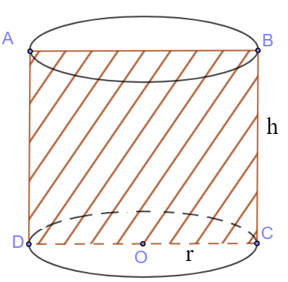Diện tích thiết diện:

SABCD = BC.CD =2r.h

Cắt hình trụ bởi mặt phẳng (P) song song và cách trục một khoảng x

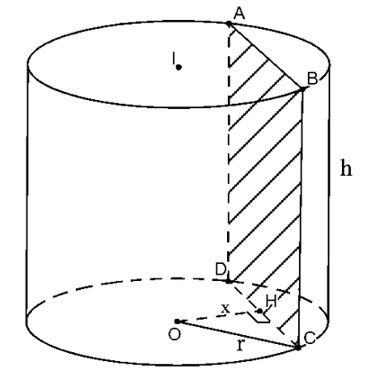Thiết diện tạo thành là hình chữ nhật ABCD như hình trên.

Gọi H là trung điểm CD ta có OH ⊥ CD=>

$CD=2\sqrt{r^2-x^2}$

Do đó diện tích thiết diện

$S_{ABCD}=CD.BC=2h\sqrt{r^2-x^2}$

Cắt hình trụ bởi mặt phẳng (P) không vuông góc với trục nhưng cắt tất cả các đường sinh của hình trụ

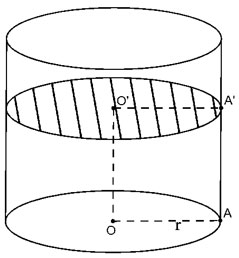Thiết diện tạo thành là hình tròn tâm O’ bán kính O'A'=r

Diện tích thiết diện: S= πr2

Cắt hình trụ bởi mặt phẳng (P) không vuông góc với trục nhưng cắt tất cả các đường sinh của hình trụ.

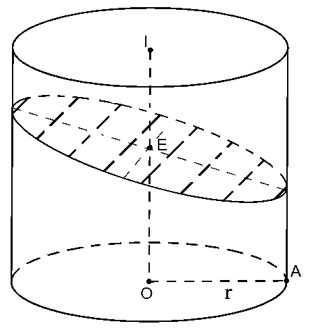Thiết diện tạo thành là Elip (E) có trục nhỏ 2r => a=r

Trục lớn bằng

với là góc giữa trục OI với (P)

Do đó diện tích S= π. a.b=

Ví dụ tính diện tích hình trụ

Bài 1:

Diện tích xung quanh của một hình trụ có chu vi hình tròn đáy là 13cm và chiều cao là 3cm.

Giải:

Ta có: chu vi hình tròn C = 2R.π = 13cm, h = 3cm

Vậy diện tích xung quanh của hình trụ là :

Sxq = 2πr.h = C.h = 13.3 = 39 (cm²)

Bài 2: Cho một hình trụ có bán kính đường tròn đáy là 6cm, trong khi đó chiều cao nối từ đáy tới đỉnh hình trụ dày 8 cm. Hỏi diện tích xung quanh và diện tích toàn phần của hình trụ bằng bao nhiêu?

Giải

Theo công thức ta có bán đường tròn đáy r = 6 cm và chiều cao của hình trụ h = 8 cm . Suy ra ta có công thức tính diện tích xung quanh hình trụ và diện tích toàn phần hình trụ bằng:

Diện tích xung quanh hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm²

Diện tích toàn phần hình trụ = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²

Bài 3: Một hình trụ có bán kính đáy là 7cm, diện tích xung quanh bằng 352cm2.

Khi đó, chiều cao của hình trụ là:

(A) 3,2 cm; (B) 4,6cm; (C) 1,8 cm

(D) 2,1cm; (E) Một kết quả khác

Hãy chọn kết quả đúng.

Giải: Ta có

$Sxq=2\pi rh\ =>\ h=\frac{Sxq}{2\pi r}=\ \frac{352}{2\pi7}=8$

Vậy, đáp án E là chính xác.

Bài 4: Chiều cao của một hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh của hình trụ 314 cm2. Hãy tính bán kính đường tròn đáy và thể tích hình trụ (làm tròn kết quả đến chữ số thập phân thứ hai).

Công thức tính thể tích hình trụ

Giải:

Diện tích xung quanh hình trụ bằng 314cm2

Ta có Sxq = 2.π.r.h = 314

Mà r = h

Nên 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (cm)

Thể tích hình trụ: V = π.r2.h = π.r3 ≈ 1109,65 (cm³).

Hy vọng bài viết trên đã giúp bạn nắm được những kiến thức cơ bản cũng như nâng cao về hình trụ, cách tính diện tích toàn phần và diện tích xung quanh của hình trụ.

Thứ Hai, 18/11/2024 20:35

3,7 ★ 151 👨 2.372.915

Bạn nên đọc

7 Bình luận

Sắp xếp theo

Xóa Đăng nhập để Gửi

Pham Ngan
hay quá ad ơi, rất dễ hiểu, em làm được rồi
Thích Phản hồi 2 29/03/22
Bích Lam
công thức tính dễ hiểu, có cả ví dụ
Thích Phản hồi 2 29/03/22
Hồng Ngát
trước đi học mình sợ mấy bài này lắm, giờ xem lại công thức thấy cg dễ phết
Thích Phản hồi 2 29/03/22
Nguyen Van Khanh
công thức đúng
Thích Phản hồi 2 29/03/22
Ngọc Khánh
hay quá, có cả diện tích và thể tích
Thích Phản hồi 1 29/03/22
Ngan Nga
thông tin rất hữu ích
Thích Phản hồi 1 29/03/22
Trần Lê Huyền Thương
hóa ra tính diện tích hình trụ lại dễ như thế
Thích Phản hồi 1 29/03/22