-

Bài tập Python có rất nhiều trên Internet nhằm giúp bạn dễ luyện code Python. Dưới đây là những bài tập Python tổng hợp kiến thức cơ bản nhất của ngôn ngữ lập trình này.
-
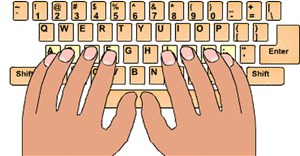
Luyện và biết gõ 10 ngón là một lợi thế lớn đối với những người làm việc trong môi trường văn phòng hằng ngày phải tiếp xúc với máy tính và soạn thảo văn bản. Hãy xem bài luyện tập gõ 10 ngón dưới đây, cố gắng nắm bắt kỹ thuật đánh máy 10 ngón này đảm bảo bạn sẽ cải thiện đáng kể tốc độ đánh máy của mình.
-

Xóa trang trắng trong Word là điều cần thực hiện để loại bỏ những trang không có nội dung trong Word, những trang trắng làm ảnh hưởng tới tài liệu và người đọc. T\
-

Tắt update Windows 10, chặn Win 10 tự động cập nhật hay tắt tính năng tự cập nhật trên Windows 10, bạn sẽ phải làm những điều này một cách thủ công vì tùy chọn tắt Update hoàn toàn không còn được tích hợp sẵn.
-
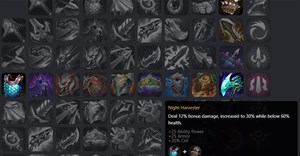
Trang bị DTCL mùa 9.5 sẽ có khá nhiều thay đổi, sẽ có nhiều trang bị ghép từ trang bị thành phần bị thay thế.
-

Dưới đây là tổng hợp một số bài tập Pascal từ cơ bản đến phức tạp mà Quantrimang.com đã tổng hợp lại, hy vọng việc học của bạn sẽ dễ dàng hơn đôi chút.
-

Đánh số trang trong Word bỏ trang đầu là thao tác đơn giản và thường được sử dụng khi chúng ta làm tài liệu, sách tham khảo, sách giáo khoa, giáo án,...
-

Bạn muốn tăng tốc Windows 10, cải thiện tốc độ Windows 10 hay tăng tốc khởi động Windows 10? Mọi cách tăng tốc Windows 10 đều có trong bài viết này, bạn hãy đọc và áp dụng để máy tính Windows 10 chạy nhanh hơn nhé!
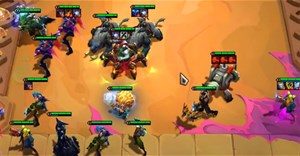 Đồ mới DTCL mùa 9 sẽ chỉ thay đổi Ấn Hệ Tộc và chỉ số của một vài trang bị cũ cùng với trang bị của Ornn.
Đồ mới DTCL mùa 9 sẽ chỉ thay đổi Ấn Hệ Tộc và chỉ số của một vài trang bị cũ cùng với trang bị của Ornn. Nếu Reset Win 10, bạn cần biết một số tùy chọn để tránh việc bị xóa hết các dữ liệu trên máy tính. Trong bài viết này, Quantrimang.com sẽ chỉ rõ cho bạn cách để reset máy tính về trạng thái ban đầu và ý nghĩa của các tùy chọn reset máy.
Nếu Reset Win 10, bạn cần biết một số tùy chọn để tránh việc bị xóa hết các dữ liệu trên máy tính. Trong bài viết này, Quantrimang.com sẽ chỉ rõ cho bạn cách để reset máy tính về trạng thái ban đầu và ý nghĩa của các tùy chọn reset máy. Bài tập Python có rất nhiều trên Internet nhằm giúp bạn dễ luyện code Python. Dưới đây là những bài tập Python tổng hợp kiến thức cơ bản nhất của ngôn ngữ lập trình này.
Bài tập Python có rất nhiều trên Internet nhằm giúp bạn dễ luyện code Python. Dưới đây là những bài tập Python tổng hợp kiến thức cơ bản nhất của ngôn ngữ lập trình này. Luyện và biết gõ 10 ngón là một lợi thế lớn đối với những người làm việc trong môi trường văn phòng hằng ngày phải tiếp xúc với máy tính và soạn thảo văn bản. Hãy xem bài luyện tập gõ 10 ngón dưới đây, cố gắng nắm bắt kỹ thuật đánh máy 10 ngón này đảm bảo bạn sẽ cải thiện đáng kể tốc độ đánh máy của mình.
Luyện và biết gõ 10 ngón là một lợi thế lớn đối với những người làm việc trong môi trường văn phòng hằng ngày phải tiếp xúc với máy tính và soạn thảo văn bản. Hãy xem bài luyện tập gõ 10 ngón dưới đây, cố gắng nắm bắt kỹ thuật đánh máy 10 ngón này đảm bảo bạn sẽ cải thiện đáng kể tốc độ đánh máy của mình. Xóa trang trắng trong Word là điều cần thực hiện để loại bỏ những trang không có nội dung trong Word, những trang trắng làm ảnh hưởng tới tài liệu và người đọc. T\
Xóa trang trắng trong Word là điều cần thực hiện để loại bỏ những trang không có nội dung trong Word, những trang trắng làm ảnh hưởng tới tài liệu và người đọc. T\ Tắt update Windows 10, chặn Win 10 tự động cập nhật hay tắt tính năng tự cập nhật trên Windows 10, bạn sẽ phải làm những điều này một cách thủ công vì tùy chọn tắt Update hoàn toàn không còn được tích hợp sẵn.
Tắt update Windows 10, chặn Win 10 tự động cập nhật hay tắt tính năng tự cập nhật trên Windows 10, bạn sẽ phải làm những điều này một cách thủ công vì tùy chọn tắt Update hoàn toàn không còn được tích hợp sẵn. Trang bị DTCL mùa 9.5 sẽ có khá nhiều thay đổi, sẽ có nhiều trang bị ghép từ trang bị thành phần bị thay thế.
Trang bị DTCL mùa 9.5 sẽ có khá nhiều thay đổi, sẽ có nhiều trang bị ghép từ trang bị thành phần bị thay thế. Dưới đây là tổng hợp một số bài tập Pascal từ cơ bản đến phức tạp mà Quantrimang.com đã tổng hợp lại, hy vọng việc học của bạn sẽ dễ dàng hơn đôi chút.
Dưới đây là tổng hợp một số bài tập Pascal từ cơ bản đến phức tạp mà Quantrimang.com đã tổng hợp lại, hy vọng việc học của bạn sẽ dễ dàng hơn đôi chút. Đánh số trang trong Word bỏ trang đầu là thao tác đơn giản và thường được sử dụng khi chúng ta làm tài liệu, sách tham khảo, sách giáo khoa, giáo án,...
Đánh số trang trong Word bỏ trang đầu là thao tác đơn giản và thường được sử dụng khi chúng ta làm tài liệu, sách tham khảo, sách giáo khoa, giáo án,... Bạn muốn tăng tốc Windows 10, cải thiện tốc độ Windows 10 hay tăng tốc khởi động Windows 10? Mọi cách tăng tốc Windows 10 đều có trong bài viết này, bạn hãy đọc và áp dụng để máy tính Windows 10 chạy nhanh hơn nhé!
Bạn muốn tăng tốc Windows 10, cải thiện tốc độ Windows 10 hay tăng tốc khởi động Windows 10? Mọi cách tăng tốc Windows 10 đều có trong bài viết này, bạn hãy đọc và áp dụng để máy tính Windows 10 chạy nhanh hơn nhé! Công nghệ
Công nghệ  Học CNTT
Học CNTT  Tiện ích
Tiện ích  Khoa học
Khoa học  Cuộc sống
Cuộc sống  Làng Công nghệ
Làng Công nghệ  Ứng dụng
Ứng dụng  Game - Trò chơi
Game - Trò chơi  iPhone
iPhone  Công nghệ
Công nghệ  Ứng dụng
Ứng dụng  Hệ thống
Hệ thống  Game - Trò chơi
Game - Trò chơi  iPhone
iPhone  Android
Android  Linux
Linux  Đồng hồ thông minh
Đồng hồ thông minh  Chụp ảnh - Quay phim
Chụp ảnh - Quay phim  macOS
macOS  Phần cứng
Phần cứng  Thủ thuật SEO
Thủ thuật SEO  Kiến thức cơ bản
Kiến thức cơ bản  Dịch vụ ngân hàng
Dịch vụ ngân hàng  Lập trình
Lập trình  Dịch vụ nhà mạng
Dịch vụ nhà mạng  Dịch vụ công trực tuyến
Dịch vụ công trực tuyến  Nhà thông minh
Nhà thông minh  Học CNTT
Học CNTT  Quiz công nghệ
Quiz công nghệ  Microsoft Word 2016
Microsoft Word 2016  Microsoft Word 2013
Microsoft Word 2013  Microsoft Word 2007
Microsoft Word 2007  Microsoft Excel 2019
Microsoft Excel 2019  Microsoft Excel 2016
Microsoft Excel 2016  Microsoft PowerPoint 2019
Microsoft PowerPoint 2019  Google Sheets - Trang tính
Google Sheets - Trang tính  Code mẫu
Code mẫu  Photoshop CS6
Photoshop CS6  Photoshop CS5
Photoshop CS5  Lập trình Scratch
Lập trình Scratch  Bootstrap
Bootstrap  Download
Download  Ứng dụng văn phòng
Ứng dụng văn phòng  Tải game
Tải game  Tiện ích hệ thống
Tiện ích hệ thống  Ảnh, đồ họa
Ảnh, đồ họa  Internet
Internet  Bảo mật, Antivirus
Bảo mật, Antivirus  Họp, học trực tuyến
Họp, học trực tuyến  Video, phim, nhạc
Video, phim, nhạc  Giao tiếp, liên lạc, hẹn hò
Giao tiếp, liên lạc, hẹn hò  Hỗ trợ học tập
Hỗ trợ học tập  Máy ảo
Máy ảo  Tiện ích
Tiện ích  Khoa học
Khoa học  Điện máy
Điện máy  Tủ lạnh
Tủ lạnh  Tivi
Tivi  Điều hòa
Điều hòa  Máy giặt
Máy giặt  Quạt các loại
Quạt các loại  Cuộc sống
Cuộc sống  Kỹ năng
Kỹ năng  Món ngon mỗi ngày
Món ngon mỗi ngày  Làm đẹp
Làm đẹp  Nuôi dạy con
Nuôi dạy con  Chăm sóc Nhà cửa
Chăm sóc Nhà cửa  Du lịch
Du lịch  Mẹo vặt
Mẹo vặt  Giáng sinh - Noel
Giáng sinh - Noel  Quà tặng
Quà tặng  Giải trí
Giải trí  Là gì?
Là gì?  Nhà đẹp
Nhà đẹp  TOP
TOP  Ô tô, Xe máy
Ô tô, Xe máy  Giấy phép lái xe
Giấy phép lái xe  Làng Công nghệ
Làng Công nghệ  Tấn công mạng
Tấn công mạng  Chuyện công nghệ
Chuyện công nghệ  Công nghệ mới
Công nghệ mới  Trí tuệ nhân tạo (AI)
Trí tuệ nhân tạo (AI)  Anh tài công nghệ
Anh tài công nghệ  Bình luận công nghệ
Bình luận công nghệ