Một số thuật toán mã hóa khối đối xứng quan trọng được sử dụng hiện tại được dựa trên cấu trúc được gọi là mật mã khối Feistel [FEIS73]. Vì lý do đó, điều quan trọng là kiểm tra các nguyên tắc thiết kế của mật mã Feistel.
Trong phần này, chúng ta bắt đầu với một so sánh về Stream Cipher và Block Cipher. Sau đó, chúng ta thảo luận về cấu trúc mật mã khối Feistel.
Stream Ciphers và Block Ciphers
Stream Cipher là loại mã hóa luồng dữ liệu số một bit hoặc một byte mỗi lần. Ví dụ về stream cipher cổ điển là mật mã Vigenère tự động và mật mã Vernam. Trong trường hợp lý tưởng, phiên bản one-time pad. của mật mã Vernam sẽ được sử dụng, trong đó keystream (ki) dài bằng số bit plaintext (pi).
Nếu keystream mật mã là ngẫu nhiên, thì mật mã này không thể bị phá vỡ bằng bất kỳ phương tiện nào khác ngoài việc có được keystream. Tuy nhiên, keystream phải được cung cấp cho cả hai phía người dùng trước thông qua một số kênh độc lập và an toàn. Điều này dẫn đến một số vấn đề không thể sử dụng đối với dữ liệu lớn
Theo đó, vì lý do thực tế, trình tạo bit-stream phải được xem là một thủ tục thuật toán, vì vậy bit-stream mã hoá có thể được sản xuất bởi cả hai phía người dùng. Bộ tạo bit-stream là một thuật toán được điều khiển bằng khóa và phải tạo ra một bit-stream mạnh về mặt mã hoá. Nghĩa là, phải tính toán không thực tế để dự đoán các phần trong tương lai của bit-stream dựa trên các phần trước của bit-stream. Hai người dùng chỉ cần chia sẻ khóa tạo và mỗi người có thể tạo ra keystream.
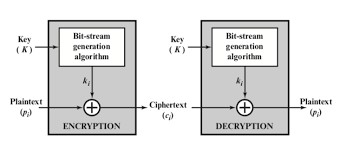
Block Cipher là một khối trong đó một khối plaintext được coi là khối văn bản gốc cần được xử lý và được sử dụng để tạo ra một khối cipher text có độ dài bằng nhau. Thông thường, kích thước khối 64 hoặc 128 bit được sử dụng, giống như với Stream Cipher, hai người dùng chia sẻ khóa mã hóa đối xứng.
Sử dụng một số chế độ hoạt động, một Block Cipher có thể được sử dụng để đạt được hiệu quả tương tự như Stream Cipher. Cần nhiều nỗ lực hơn nữa để đi vào phân tích mật mã khối, nhìn chung, Block cipher dường như có thể áp dụng cho một phạm vi ứng dụng rộng hơn so với Stream Cipher. Phần lớn các ứng dụng mã hóa đối xứng dựa trên mạng sử dụng Block Cipher.
Cấu trúc mật mã Feistel
Một mật mã khối hoạt động trên một khối plaintext gồm n bit để tạo ra một khối ciphertext gồm n bit. Có 2^n khối plaintext khác nhau có thể và để mã hóa có thể đảo ngược (nghĩa là để giải mã được), mỗi khối phải tạo ra một khối ciphertext duy nhất. Một chuyển đổi như vậy được gọi là đảo ngược, hoặc không có nghĩa. Các ví dụ sau đây minh họa các phép biến đổi không đặc trưng và số ít cho n = 2.
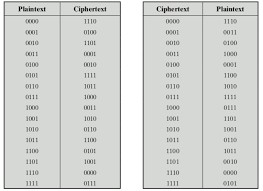
Trong trường hợp sau, một ciphertext của 01 có thể được tạo bởi một trong hai khối văn bản thuần túy. Vì vậy, nếu chúng ta giới hạn reversible mapping, số lượng biến đổi khác nhau là (2n!)^2.
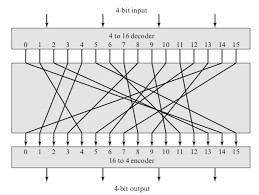
Hình trên minh họa logic của một mật mã thay thế chung cho n = 4. Một đầu vào 4 bit tạo ra một trong 16 trạng thái đầu vào có thể, được ánh xạ bởi mật mã phụ vào một trong 16 trạng thái đầu ra có thể, mỗi trạng thái được lặp lại - được gửi bởi 4 bit plaintext.
Ánh xạ mã hóa và giải mã có thể được xác định bằng cách lập bảng, như bảng dưới đây:
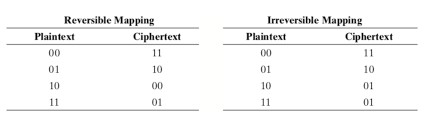
Feistel gọi đây là “idea block cipher”. Bởi vì nó cho phép số lượng ánh xạ mã hóa tối đa có thể có từ khối plaintext. Nhưng có một vấn đề thực tế với “idea block cipher”. Nếu kích thước khối nhỏ, chẳng hạn như n = 4, được sử dụng, thì hệ thống tương đương với mật mã thay thế cổ điển.
Các hệ thống như vậy, như chúng ta đã thấy, dễ bị tấn công khi phân tích thống kê về plaintext. Điểm yếu này không phải là cố hữu trong việc sử dụng mật mã thay thế mà là kết quả của việc sử dụng kích thước khối nhỏ. Nếu n đủ lớn và sự thay thế có thể đảo ngược tùy ý giữa plaintext và cipher được cho phép, thì các đặc điểm thống kê của plaintext gốc được che giấu đến mức mà loại phân tích mật mã này không khả thi.
Tuy nhiên, một mật mã thay thế có thể đảo ngược tùy ý (mật mã khối lý tưởng) cho kích thước khối lớn là không thực tế, tuy nhiên, từ quan điểm thực hiện và hiệu suất. Đối với một chuyển đổi như vậy, chính ánh xạ tạo thành khóa. Xem xét lại bảng chuyển đổi phía trên, định nghĩa một ánh xạ đảo ngược cụ thể từ plaintext sang ciphertext cho n = 4.
Ánh xạ có thể được xác định bởi các mục trong cột thứ hai, hiển thị giá trị của ciphertext cho mỗi khối plaintext. Về bản chất, đây là chìa khóa xác định ánh xạ cụ thể trong số tất cả các ánh xạ có thể. Trong trường hợp này, sử dụng phương pháp xác định khóa đơn giản này, độ dài khóa cần thiết là (4 bit) * (16 rows) = 64 bit.
Nói chung, đối với một mật mã khối lý tưởng n bit, độ dài của khóa được xác định theo kiểu này là n * (2^n) bit. Đối với khối 64 bit, có độ dài mong muốn để ngăn chặn các cuộc tấn công thống kê, độ dài khóa cần thiết là 64 * (2^64) = 2^70 tương đương 10^21 bit.
Feistel Cipher
Feistel đã đề xuất rằng chúng ta có thể tính gần đúng “idea block cipher” bằng cách sử dụng khái niệm về “product cipher”, đó là việc thực hiện hai hoặc nhiều loại mã hoá đơn giản theo cách sao cho kết quả cuối cùng hoặc sản phẩm được mã hóa mạnh hơn bất kỳ mã hoá thành phần nào. Bản chất của phương pháp này là phát triển một mật mã khối với độ dài khóa là k bit và chiều dài khối là n bit, cho phép tổng cộng 2^k biến đổi có thể, thay vì (2^n)! biến đổi có sẵn với “idea block cipher”.
Cụ thể, Feistel đề xuất sử dụng một mã hoá thay thế các thay thế và hoán vị, trong đó các thuật ngữ này được định nghĩa như sau:
- Substitution (Thay thế): Mỗi thành phần hoặc nhóm yếu tố văn bản gốc được thay thế duy nhất bằng một yếu tố mã hóa tương ứng hoặc nhóm các yếu tố mã hoá liên quan.
- Permutation (Hoán vị): Một chuỗi các thành phần của văn bản được thay thế bằng hoán vị của chuỗi đó. Đó là, không có phần tử nào được thêm hoặc xóa hoặc thay thế trong chuỗi, thay vào đó là thứ tự các phần tử xuất hiện trong chuỗi được thay đổi.
Kiến trúc bên trong của Feistel Cipher
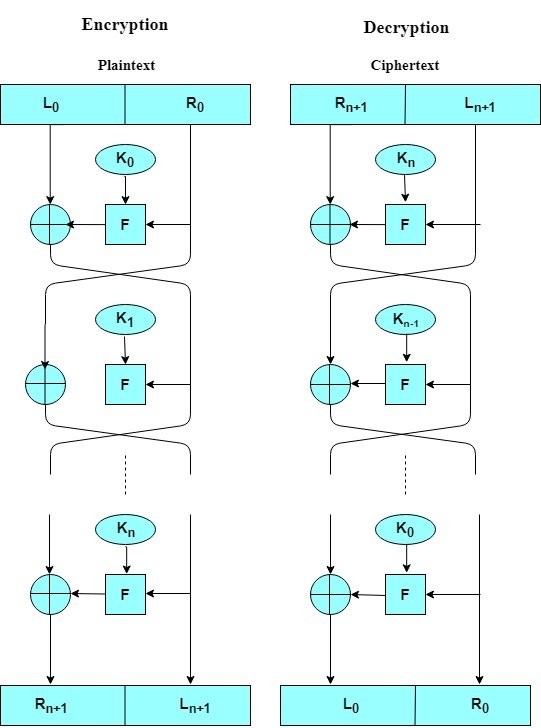
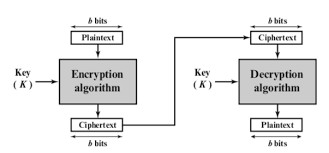
Phía bên trái của hình trên mô tả cấu trúc mã hóa được đề xuất bởi Feistel. Các đầu vào của thuật toán mã hóa là một khối văn bản có độ dài 2w bit và khóa K. Khối plaintext được chia thành hai nửa, LE0 và RE0. Hai nửa dữ liệu đi qua n vòng xử lý và sau đó kết hợp để tạo ra khối ciphertext.
Mỗi vòng i có đầu vào LEi - 1 và REi - 1 xuất phát từ vòng trước, cũng như một khóa con Ki có nguồn gốc từ tất cả K. Nói chung, các khóa con Ki khác với K và khác nhau. Trong hình trên, 16 round được sử dụng, mặc dù số lượng round có thể được thực hiện nhiều hơn.
Tất cả các round có cấu trúc giống nhau. Một substitution(Thay thế) được thực hiện ở nửa bên trái của dữ liệu. Điều này được thực hiện bằng cách áp dụng 1 round function F cho nửa bên phải của dữ liệu và sau đó lấy exclusive-OR của đầu ra của chức năng đó và nửa bên trái của dữ liệu.
Round function có cấu trúc chung giống nhau cho mỗi round nhưng được tham số hóa bởi khóa con Ki. Một cách khác để diễn đạt điều này là nói rằng F là một hàm của nửa bit bên phải và một khóa con của các bit y, tạo ra giá trị đầu ra có độ dài w bit: F (REi, Ki + 1).
Sau substitution này, một permutation (hoán vị) được thực hiện bao gồm sự trao đổi của hai nửa dữ liệu. Cấu trúc này là một dạng đặc biệt của mạng hoán vị thay thế (SPN) do Shannon đề xuất.
Việc thực hiện chính xác mạng Feistel phụ thuộc vào việc lựa chọn các tham số và tính năng thiết kế sau:
- Block size: Block size lớn hơn có nghĩa là bảo mật cao hơn (tất cả những thứ khác đều bằng nhau) nhưng giảm tốc độ encrypt/decrypt cho một thuật toán nhất định. Bảo mật hơn đạt được bằng sự khuếch tán lớn hơn. Theo truyền thống, kích thước khối 64 bit đã được coi là sự đánh đổi hợp lý và gần như phổ biến trong thiết kế block cipher. Tuy nhiên, AES mới sử dụng kích thước khối 128 bit.
- Key size: Key size lớn hơn có nghĩa là bảo mật cao hơn nhưng có thể làm giảm tốc độ encrypt/decrypt. Bảo mật cao hơn đạt được nhờ khả năng chống lại các cuộc tấn công brute-force. Kích thước khóa từ 64 bit trở xuống hiện được coi là không đủ và 128 bit đã trở thành kích thước phổ biến.
- Số round: Bản chất của mật mã Feistel là một round duy nhất cung cấp bảo mật không đầy đủ nhưng nhiều round cung cấp bảo mật càng tăng lên. Số round điển hình là 16 vòng.
- Thuật toán tạo khóa con: Độ phức tạp lớn hơn trong thuật toán này sẽ dẫn đến khó khăn hơn về “cryptanalysis”.
Có hai cân nhắc khác trong thiết kế mật mã Feistel:
- Fast software encryption/decryption: Trong nhiều trường hợp, mã hóa được nhúng trong các ứng dụng hoặc chức năng tiện ích theo cách ngăn chặn việc triển khai phần cứng. Theo đó, tốc độ thực hiện của thuật toán trở thành một mối quan tâm lớn.
- Dễ phân tích: Mặc dù chúng ta muốn làm cho thuật toán của chúng ta trở nên khó khăn nhất có thể để mã hóa, nhưng có lợi ích lớn trong việc làm cho thuật toán dễ dàng phân tích. Nếu thuật toán có thể được giải thích chính xác và rõ ràng, việc phân tích thuật toán đó cho các lỗ hổng “cryptanalysis” sẽ dễ dàng hơn và do đó phát triển mức độ đảm bảo cao hơn về độ mạnh của nó. Ví dụ, DES không có chức năng dễ dàng để bị phân tích.
Trên đây là cơ sở về Block Cipher, nguồn gốc cũng như mô tả cơ bản block cipher là gì, cách thức hoạt động cũng như hướng thiết kế một block cipher cho ứng dụng.
Loạt bài về Hệ thống mật mã cũng kết thúc tại đây. Quản Trị Mạng hy vọng rằng những bài viết này sẽ mang tới cho bạn những kiến thức bổ ích về mật mã, mã hóa...
 Công nghệ
Công nghệ  AI
AI  Windows
Windows  iPhone
iPhone  Android
Android  Học IT
Học IT  Download
Download  Tiện ích
Tiện ích  Khoa học
Khoa học  Game
Game  Làng CN
Làng CN  Ứng dụng
Ứng dụng 

















 Linux
Linux  Đồng hồ thông minh
Đồng hồ thông minh  macOS
macOS  Chụp ảnh - Quay phim
Chụp ảnh - Quay phim  Thủ thuật SEO
Thủ thuật SEO  Phần cứng
Phần cứng  Kiến thức cơ bản
Kiến thức cơ bản  Lập trình
Lập trình  Dịch vụ công trực tuyến
Dịch vụ công trực tuyến  Dịch vụ nhà mạng
Dịch vụ nhà mạng  Quiz công nghệ
Quiz công nghệ  Microsoft Word 2016
Microsoft Word 2016  Microsoft Word 2013
Microsoft Word 2013  Microsoft Word 2007
Microsoft Word 2007  Microsoft Excel 2019
Microsoft Excel 2019  Microsoft Excel 2016
Microsoft Excel 2016  Microsoft PowerPoint 2019
Microsoft PowerPoint 2019  Google Sheets
Google Sheets  Học Photoshop
Học Photoshop  Lập trình Scratch
Lập trình Scratch  Bootstrap
Bootstrap  Năng suất
Năng suất  Game - Trò chơi
Game - Trò chơi  Hệ thống
Hệ thống  Thiết kế & Đồ họa
Thiết kế & Đồ họa  Internet
Internet  Bảo mật, Antivirus
Bảo mật, Antivirus  Doanh nghiệp
Doanh nghiệp  Ảnh & Video
Ảnh & Video  Giải trí & Âm nhạc
Giải trí & Âm nhạc  Mạng xã hội
Mạng xã hội  Lập trình
Lập trình  Giáo dục - Học tập
Giáo dục - Học tập  Lối sống
Lối sống  Tài chính & Mua sắm
Tài chính & Mua sắm  AI Trí tuệ nhân tạo
AI Trí tuệ nhân tạo  ChatGPT
ChatGPT  Gemini
Gemini  Prompt
Prompt  Điện máy
Điện máy  Tivi
Tivi  Tủ lạnh
Tủ lạnh  Điều hòa
Điều hòa  Máy giặt
Máy giặt  Cuộc sống
Cuộc sống  TOP
TOP  Kỹ năng
Kỹ năng  Món ngon mỗi ngày
Món ngon mỗi ngày  Nuôi dạy con
Nuôi dạy con  Mẹo vặt
Mẹo vặt  Phim ảnh, Truyện
Phim ảnh, Truyện  Làm đẹp
Làm đẹp  DIY - Handmade
DIY - Handmade  Du lịch
Du lịch  Quà tặng
Quà tặng  Giải trí
Giải trí  Là gì?
Là gì?  Nhà đẹp
Nhà đẹp  Giáng sinh - Noel
Giáng sinh - Noel  Ô tô, Xe máy
Ô tô, Xe máy  Tấn công mạng
Tấn công mạng  Chuyện công nghệ
Chuyện công nghệ  Công nghệ mới
Công nghệ mới  Trí tuệ Thiên tài
Trí tuệ Thiên tài