Thiên văn học là một trong những ngành khoa học cổ xưa nhất trên Trái Đất, được đặt nền móng bởi những nền văn minh cổ đại, trong đó đặc biệt phải kể tới nền văn minh Hy Lạp, với vô số đóng góp mang tính cách mạng trong lịch sử phát triển của loài người nói chung. Sự xuất hiện của kính viễn vọng là thời điểm đánh dấu thiên văn học bắt đầu bước vào giai đoạn khoa học hiện đại. Còn trước đó, phương pháp nghiên cứu chủ yếu được các nhà thiên văn học cổ đại áp dụng là quan sát bằng mắt thường kết hợp với các dụng cụ thiên văn thô sơ đã được tìm thấy từ những giai đoạn còn sớm hơn nữa. Tuy nhiên, không phải vì thế mà thiên văn học thời kỳ này thiếu vắng những khám phá lớn, mà thậm chí là ngược lại.
Dưới đây là 4 khám phá thiên văn quan trọng của người Hy Lạp cổ đại, có ảnh hưởng lớn đến lịch sử khám phá vũ trụ của con người.
Các hành tinh quay quanh Mặt trời
Nhà thiên văn học và toán học Hy Lạp cổ đại Aristarchus of Samos (310 trước Công nguyên - 230 trước Công nguyên) chính là người đầu tiên đặt ra lý thuyết mô hình nhật tâm, đặt Mặt Trời ở trung tâm của vũ trụ và Trái Đất xoay quanh Mặt Trời. Ông lập luận rằng Mặt Trời chính là ngọn lửa trung tâm của vũ trụ, và các hành tinh còn lại mà con người quan sát được là những thực thể xoay quanh ngọn lửa này theo một thứ tự nhất định.

Đây là một phát hiện đáng kinh ngạc, bởi nhiều người nghĩ rằng lý thuyết Mặt Trời ở trung tâm và Trái Đất quay quanh Mặt Trời phải đến thế kỷ 16 mới được bởi Nicolaus Copernicus đưa ra. Tuy nhiên trên thực tế, Nicolaus Copernicus là người đã nêu ra hình thức hiện đại đầu tiên của thuyết nhật tâm trong cuốn sách do chính ông chắp bút, và người “truyền cảm hứng” cho Nicolaus phát triển tác phẩm chính là Aristarchus of Samos.
Kích thước của mặt trăng
Tiếp tục là một khám phá quan trọng của Aristarchus of Samos. Ông là người đầu tiên đặt ra lý thuyết về kích cỡ và khoảng cách của Mặt trời và Mặt trăng. Đồng thời đưa ra các tính toán cơ bản nhất về kích thước và khoảng cách tương đối với Mặt Trời và Mặt Trăng, đặt nền móng cho nhiều phép đo quan trọng sau này.
Từ lâu, người ta đã quan sát thấy Mặt Trời và Mặt Trăng dường như có cùng kích thước trên bầu trời và Mặt trời ở xa hơn. Aristarchus nhận ra điều này sau khi chứng kiến hiện tượng nhật thực, xuất hiện khi Mặt Trăng đi qua phía trước Mặt Trời ở một khoảng cách nhất định so với Trái Đất.
Ngoài ra, khi quan sát Mặt Trăng ở các quý đầu tiên hoặc thứ ba trong năm, Aristarchus đã phát hiện ra rằng Mặt Trời, Trái Đất và Mặt Trăng sẽ tạo thành một hình tam giác vuông.
Vì Pythagoras đã xác định được độ dài của các cạnh tam giác có liên quan như thế nào trong vài thế kỷ trước đó (định lý py-ta-go), Aristarchus đã sử dụng định lý tam giác vuông để ước tính rằng khoảng cách từ Trái Đất tới Mặt Trời nằm trong khoảng từ 18 đến 20 lần so với từ Mặt Trăng. Ông cũng tính toán rằng kích thước của Mặt trăng bằng xấp xỉ 1/3 so với Trái đất, dựa trên thời gian xảy ra hiện tượng nguyệt thực toàn phần.
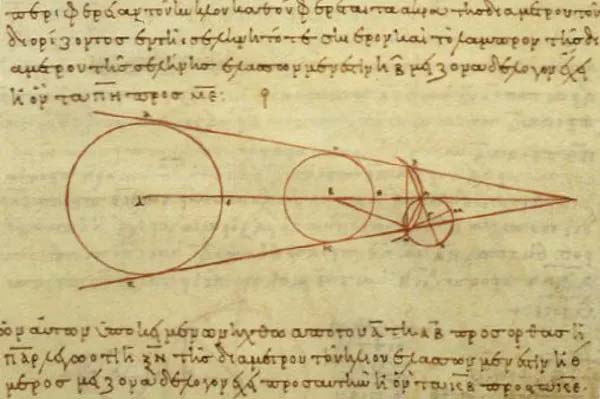
Về bài toán khoảng cách giữa Mặt trời và Mặt trăng, con số mà Áitarchus đưa ra quá thấp, trên thực tế là 390. Tuy nhiên, giá trị tỷ lệ kích thước của Trái Đất so với Mặt Trăng mà ông đưa ra lại chính xác đáng ngạc nhiên (Mặt trăng có đường kính chỉ bằng 0,27 lần (gần 1/3) so với Trái đất).
Chu vi của Trái Đất
Eratosthenes (276 trước Công nguyên - 195 trước Công nguyên) là một nhà thực nghiệm thiên văn sắc sảo của nền văn minh Hy Lạp, và một trong những thành tựu để đời của ông chính là phép tính sớm nhất về chu vi của Trái Đất. Phương pháp tính của Eratosthenes dựa trên việc đo chiều dài bóng đổ của những cây cột đặt thẳng đứng trên mặt đất vào giữa trưa ngày hạ chí, ở các vĩ độ khác nhau.
Mặt trời nằm cách xa đến nỗi ở bất cứ vị trí nào mà ánh nắng chạm tới Trái đất, chúng đều gần như ở phương song song. Vì vậy, sự khác biệt của bóng nắng của vật thể đã cho thấy bề mặt Trái đất cong đến mức nào. Eratosthenes đã sử dụng lý thuyết này để ước tính chu vi Trái Đất, và kết quả mà ông đưa ra là khoảng 40.000km - con số rất chính xác.

Một nhà thiên văn học cổ đại khác có tên Posidonius (135 trước Công nguyên - 51 trước Công nguyên) đã sử dụng một phương pháp tính toán mới, nhưng cũng đưa ra được kết quả tương tự. Posidonius sống trên đảo Rhodes trong phần lớn cuộc đời. Ở đó, ông thường quan sát thấy ngôi sao Canopus nằm rất gần đường chân trời. Tuy nhiên, khi chuyển tới sinh sống tại Alexandria, Ai Cập, Posidonius nhận thấy rằng vị trí của Canopus đã có sự thay đổi, tăng lên khoảng 7,5 độ so với đường chân trời.
Cho rằng 7,5 độ là 1/48 của một vòng tròn, Posidonius đã nhân khoảng cách từ Rhodes đến Alexandria lên 48 và đi đến một giá trị cũng xấp xỉ 40.000km - chu vi của Trái Đất.
Máy tính thiên văn đầu tiên
Máy tính cơ học tồn tại lâu đời nhất thế giới là Antikythera Mechanism, được phát hiện trong một chiếc tàu cổ bị đắm ở ngoài khơi đảo Antikythera của Hy Lạp vào năm 1900.
Thiết bị này đã bị hư hại theo thời gian, nhưng khi còn nguyên vẹn, nó mang hình dạng một chiếc hộp chứa hàng chục bánh răng bằng đồng được gia công tinh xảo. Khi xoay bằng tay một cách thủ công, các bánh răng quay số ở bên ngoài sẽ hiển thị các chu kỳ của Mặt trăng, thời gian nguyệt thực và vị trí của 5 hành tinh khác nhau được biết đến vào thời điểm đó, bao gồm Sao Thủy, Sao Kim, Sao Hỏa, Sao Mộc và Sao Thổ, theo từng mốc thời gian trong năm.

Hiện vẫn chưa rõ ai là tác giả của chiếc máy tính thiên văn độc đáo này. Tuy nhiên theo đánh giá của các nhà khoa học, nó có niên đại từ thế kỷ thứ 3 đến thế kỷ thứ 1 trước Công nguyên, và thậm chí có thể là tác phẩm của Archimedes.
 Công nghệ
Công nghệ  Windows
Windows  iPhone
iPhone  Android
Android  Học CNTT
Học CNTT  Download
Download  Tiện ích
Tiện ích  Khoa học
Khoa học  Game
Game  Làng CN
Làng CN  Ứng dụng
Ứng dụng 











 Linux
Linux  Đồng hồ thông minh
Đồng hồ thông minh  Chụp ảnh - Quay phim
Chụp ảnh - Quay phim  macOS
macOS  Phần cứng
Phần cứng  Thủ thuật SEO
Thủ thuật SEO  Kiến thức cơ bản
Kiến thức cơ bản  Dịch vụ ngân hàng
Dịch vụ ngân hàng  Lập trình
Lập trình  Dịch vụ nhà mạng
Dịch vụ nhà mạng  Dịch vụ công trực tuyến
Dịch vụ công trực tuyến  Nhà thông minh
Nhà thông minh  Quiz công nghệ
Quiz công nghệ  Microsoft Word 2016
Microsoft Word 2016  Microsoft Word 2013
Microsoft Word 2013  Microsoft Word 2007
Microsoft Word 2007  Microsoft Excel 2019
Microsoft Excel 2019  Microsoft Excel 2016
Microsoft Excel 2016  Microsoft PowerPoint 2019
Microsoft PowerPoint 2019  Google Sheets - Trang tính
Google Sheets - Trang tính  Code mẫu
Code mẫu  Photoshop CS6
Photoshop CS6  Photoshop CS5
Photoshop CS5  Lập trình Scratch
Lập trình Scratch  Bootstrap
Bootstrap  Ứng dụng văn phòng
Ứng dụng văn phòng  Tải game
Tải game  Tiện ích hệ thống
Tiện ích hệ thống  Ảnh, đồ họa
Ảnh, đồ họa  Internet
Internet  Bảo mật, Antivirus
Bảo mật, Antivirus  Họp, học trực tuyến
Họp, học trực tuyến  Video, phim, nhạc
Video, phim, nhạc  Giao tiếp, liên lạc, hẹn hò
Giao tiếp, liên lạc, hẹn hò  Hỗ trợ học tập
Hỗ trợ học tập  Máy ảo
Máy ảo  Điện máy
Điện máy  Tủ lạnh
Tủ lạnh  Tivi
Tivi  Điều hòa
Điều hòa  Máy giặt
Máy giặt  Quạt các loại
Quạt các loại  Cuộc sống
Cuộc sống  Kỹ năng
Kỹ năng  Món ngon mỗi ngày
Món ngon mỗi ngày  Làm đẹp
Làm đẹp  Nuôi dạy con
Nuôi dạy con  Chăm sóc Nhà cửa
Chăm sóc Nhà cửa  Du lịch
Du lịch  Halloween
Halloween  Mẹo vặt
Mẹo vặt  Giáng sinh - Noel
Giáng sinh - Noel  Quà tặng
Quà tặng  Giải trí
Giải trí  Là gì?
Là gì?  Nhà đẹp
Nhà đẹp  TOP
TOP  Ô tô, Xe máy
Ô tô, Xe máy  Giấy phép lái xe
Giấy phép lái xe  Tấn công mạng
Tấn công mạng  Chuyện công nghệ
Chuyện công nghệ  Công nghệ mới
Công nghệ mới  Trí tuệ nhân tạo (AI)
Trí tuệ nhân tạo (AI)  Anh tài công nghệ
Anh tài công nghệ  Bình luận công nghệ
Bình luận công nghệ